In each situation of Column - I, two electric dipoles having dipole moments →p1and→p2 of same magnitude (that is,p1=p2) are placed on x-axis symmertrically about origin in different orientations as shown. In column - II certain inferences are drawn for these two dipoles. Then match the different orientations of dipoles in column - I with the corresponding results in column - II. [In column I the co-ordinates corresponding to the centres of dipoles and dipoles having the same dipole lenght]

The correct Answer is:A, B, C, D
Topper's Solved these Questions
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - LECTURE SHEET (EXERCISE - V) (LEVEL - II (ADVANCED) INTEGER TYPE QUESTIONS)
1 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE - I COULOMB.S INVERSE SQUARE LAQW) (LEVEL -I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTION
5 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - LECTURE SHEET (EXERCISE - V) (LEVEL - II (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)
3 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
6 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
9 Videos
Similar Questions
In each situation of Column-I two elelctric dipoles having moments →p1 and →p1 of same magnitude (that is ,p1=p2) are placed on x-axis symmetrically about origin in different orientations as shown. In column-II certain inferences are drawn for these two dipoles. Then match the different orientations of dipole in column-I with the corresponding result in column-II.

View SolutionColumn-I shows different charge distributions. Cloumn-II gives corresponding electric dipole moments.
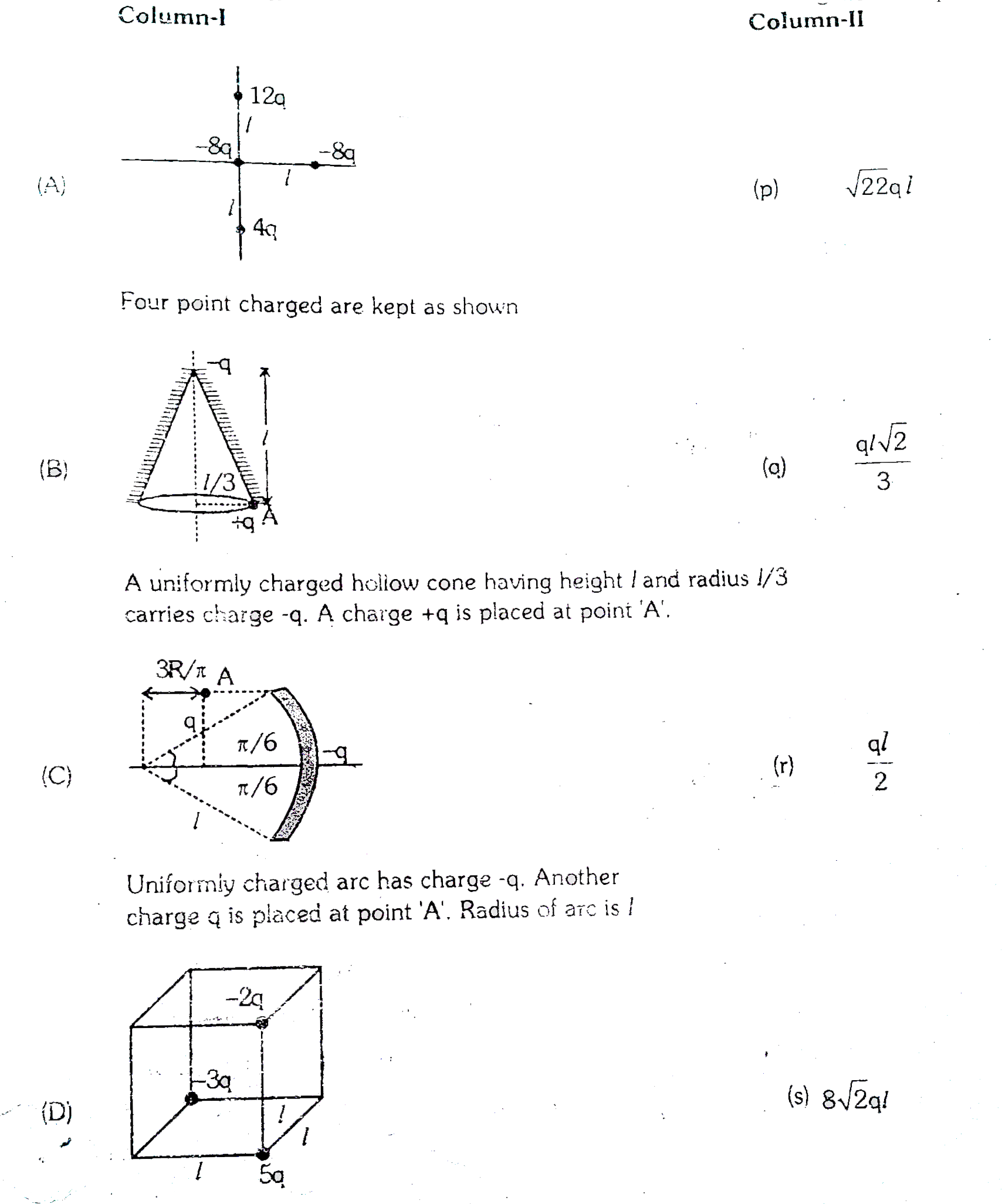
View Solution
Knowledge Check
The torque τ acting on an electric dipole of dipole momtn →pin an electric field →E is
A→τ=→p.→EB→τ=→p×→EC→τ=p.→ED→τ=→pETwo point dipoles of dipole moment →p1and→p2 are at a distance x from each other and →p1∣∣→p2 . The force between the dipoles is :
A14πε04p1p2x4B14πε03p1p2x3C14πε06p1p2x4D14πε08p1p2x4The electric field intensity →E , , due to an electric dipole of dipole moment →p , at a point on the equatorial line is :
Aparallel to the axis of the dipole and opposite to the direction of dipole momentBperpendicular to the axis of the dipole and is directed away from itCparallel to the dipole momentDperpendicular to the axis of the dipole and is directed towards it
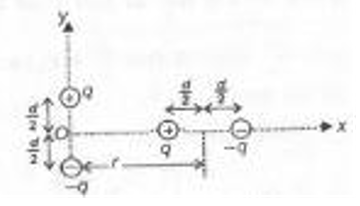
Two identical electric dipoles of dipole moments p are placed as shown in the figure. The electrostatic force on dipole placed along x-axis is (d << r) (14πε0 )
View SolutionGiven below are two columns – Column I and Column II. Match each item of Column I with the corresponding item of Column II.

View Solutionin column - I certain situations are shown Column-II has different values of phase difference Match them [take π2=10 wherever required]


View SolutionTwo short electric dipoles having dipole moment p1 and p2 are placed co-axially and uni-directionally, at a distance r apart. Calculate nature and magnitude of force between them :
View SolutionThe electric field intensity →E , , due to an electric dipole of dipole moment →p , at a point on the equatorial line is :
View Solution
