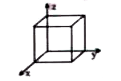
Electric field in a region is given by →E=−4xˆi+6yˆj. Then find the charge enclosed in the cube of side 1m oriented as shown in the diagram
 Solution in Telugu
Solution in Telugu
ε0
2ε0
3ε0
10ε0
The correct Answer is:B
Step by step video, text & image solution for Electric field in a region is given by vec( E) = - 4xhat(i) + 6yhat(j). Then find the charge enclosed in the cube of side 1m oriented as shown in the diagram by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
5 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)
2 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - I (MAIN) (STRAIGHT OBJECTIVE TYPE QUESTIONS)
24 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
6 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
9 Videos
Similar Questions
Two point - like chargesQ1andQ2 are positioned at point 1 and 2 respectively. The field intensity to the right of the charge Q3 on the line that passes through the two charges varies according to a law that is represented schematically in the figure. The field intensity is assumed to be positive if its direction with the positive direction on the x-axis. The distance between the charges is l, then which of the folllowing is true

View SolutionAn empty thick conducting shell of inner radius a and outer radius b is shown in figure. If it is obseved that the inner face of the carries a uniform charge density −σ and the surface carries a uniform charge density .σ.

If a point charge qA is placed at the center of the shell, then choose the correct statement(s)
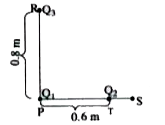
View SolutionTwo charges Q1andQ2 Coulombs are shown in fig. A third charge Q3 coulomb is moved from point R to S along a circular path with P as centre Change in potential energy is
View SolutionWhat is the radius of the path of an electron (mass 9 × 10-31 kg and charge 1.6×x10–19 C) moving at a speed of 3×x107 m/s in a magnetic field of 6x×10−4 T perpendicular to it? What is its frequency? Calculate its energy in keV. (1eV=1.6×10−19J)
View SolutionFind the components of vector ¯¯¯A=2ˆi+3ˆj along the directions of ˆi+ˆjandˆi−ˆj
View SolutionAn electric field given by vec(E )= 4hat(i)+3(y^(2)+2)hat(j) pieces Gaussian cube side 1m placed at origin such that is three sides represents x,y and z axis. This net charge enclosed within the cube is
View SolutionAn electric field is given by →E=(yˆi+xˆj)NC. Find the work done (in J) in moving a 1C charge from →rA=(2ˆi+2ˆj) m to →rB=(4ˆi+ˆj)m.
View SolutionElectric field in a region is given by vec(E)=-4xhat(i)+6yhat(j) . The charge enclosed in the cube of side 1 m oriented as shown in the diagram is given by alpha in_(0) . Find the value of alpha .
View SolutionAn electric field given by vec(E)=4hat(i)+3(y^(2)+2) hat(j) pierces a gaussian cube of side 1m placed at origin such that one of its corners is at origin and rest of sides are along positive side of coordinate axis. Find the magnitude of net charge enclosed within the cube [3 in_(0)]
View SolutionA cube has sides of length L=0.2 m It is placed with one corner at the origin as shown in figure The electric field in uniform and given by vec(E)=(2.5hat(i)-4.2hat(j))N//C .Find the electric flux through the entire cube.
View SolutionElectric field in a region of space is given by vec E=ayhat i+axhat j then
View SolutionA non-uniform electric field E=(5xhat i+3hat j)N/C goes through a cube of side length 2.0m oriented as shown. Then,
View SolutionThe electric field in a certain region is given by →E=(Kx3)→i. The dimensions of K are -
View SolutionGiven the electric field in the region vec(E ) = 2xi , find the net electric flux through the cube and enclosed by it.
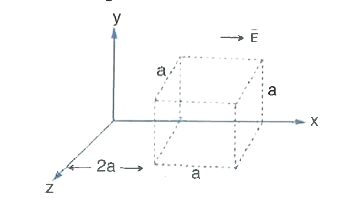
View SolutionIn a region, electric field depends on X-axis as E=E0x2. There is a cube of edge a as shown. Then find the charge enclosed in that cube.

View SolutionIn a region, electric field depends on X-axis as E≈E0x2. There is a club of edge a as shown. Then find the charge enclosed in the cube.
View Solution
