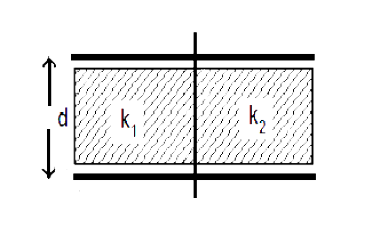
A capacitor is formed by two square metal-plates of edge a, separated by a distance d. Dielectrics of dielectric constants K1andK2 are filled in the gap as shown in fig. Find the capacitance.

ε0K1K2a2ln(K1K2)(K1−K2)d
ε0(K1+K2)a2ln(K1K2)(K1−K2)d
ε0(K1+K2)a2ln(K2K1)(K1−K2)d
ε0K1K2a2ln(K2K1)(K1−K2)d
The correct Answer is:A
Topper's Solved these Questions
- CAPACITORS BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - LECTURE SHEET (EXERCISE - IV) (LEVEL - II (ADVANCED)) (More than one correct answer Type Questions )
3 Videos
- CAPACITORS BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - LECTURE SHEET (EXERCISE - IV) (LEVEL - II (ADVANCED)) (Matrix Matching Type Questions)
1 Videos
- CAPACITORS BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - LECTURE SHEET (EXERCISE - IV) (LEVEL - I (MAIN)) Straight Objective Type Questions)
8 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
- COMMUNICATION SYSTEM BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEM EXERCISE - LECTURE SHEET (LEVEL - I) (MAIN) (EXERCISE - IV) (Straight Objective & More than one Correct Answer Type Questions)
20 Videos
Similar Questions
A capacitor is formed by two square metal plate of edge a,separated by a distance d.Dielectric constantsK1andK2are filled in the gap as shown in figure(31-E25).Find the capacitance.

View SolutionA capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant K1=6andK2=4. New capacitance will be

View Solution
Knowledge Check
A capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant K1=6andK2=4. New capacitance will be
 A4Aε0dB4.8Aε0dC5Aε0dD2.4Aε0d
A4Aε0dB4.8Aε0dC5Aε0dD2.4Aε0dThe capacitance of a capacitor, filled with two dielectrics of same dimensions but of dielectric constants K1andK2 respectively as shown will be -
 A∈0A2d(K1+K2)B∈0Ad(K1+K2)C∈0A2d(K1+K2K1+K2)D∈0Ad(K1K2K1+K2)
A∈0A2d(K1+K2)B∈0Ad(K1+K2)C∈0A2d(K1+K2K1+K2)D∈0Ad(K1K2K1+K2)A parallel plate capacitor has the space between its plates filled by two slabs of thickness d2 each and dielectric constant K1 and K2. d is the plate separation of the capacitor. The capacitance of the capacitor is
A2ε0Ad(K1+K2K1K2)B2ε0Ad(K1+K2)C2ε0Ad(K1K2K1+K2)D2ε0dA(K1+K2K1K2)
A paralled plate capacitor is made of two square plates of side 'a' , separated by a distance d (dltlta). The lower triangular portion is filled with a dielecttic of dielectric constant K, as shown in the figure. Capacitance of this Capacitor is :
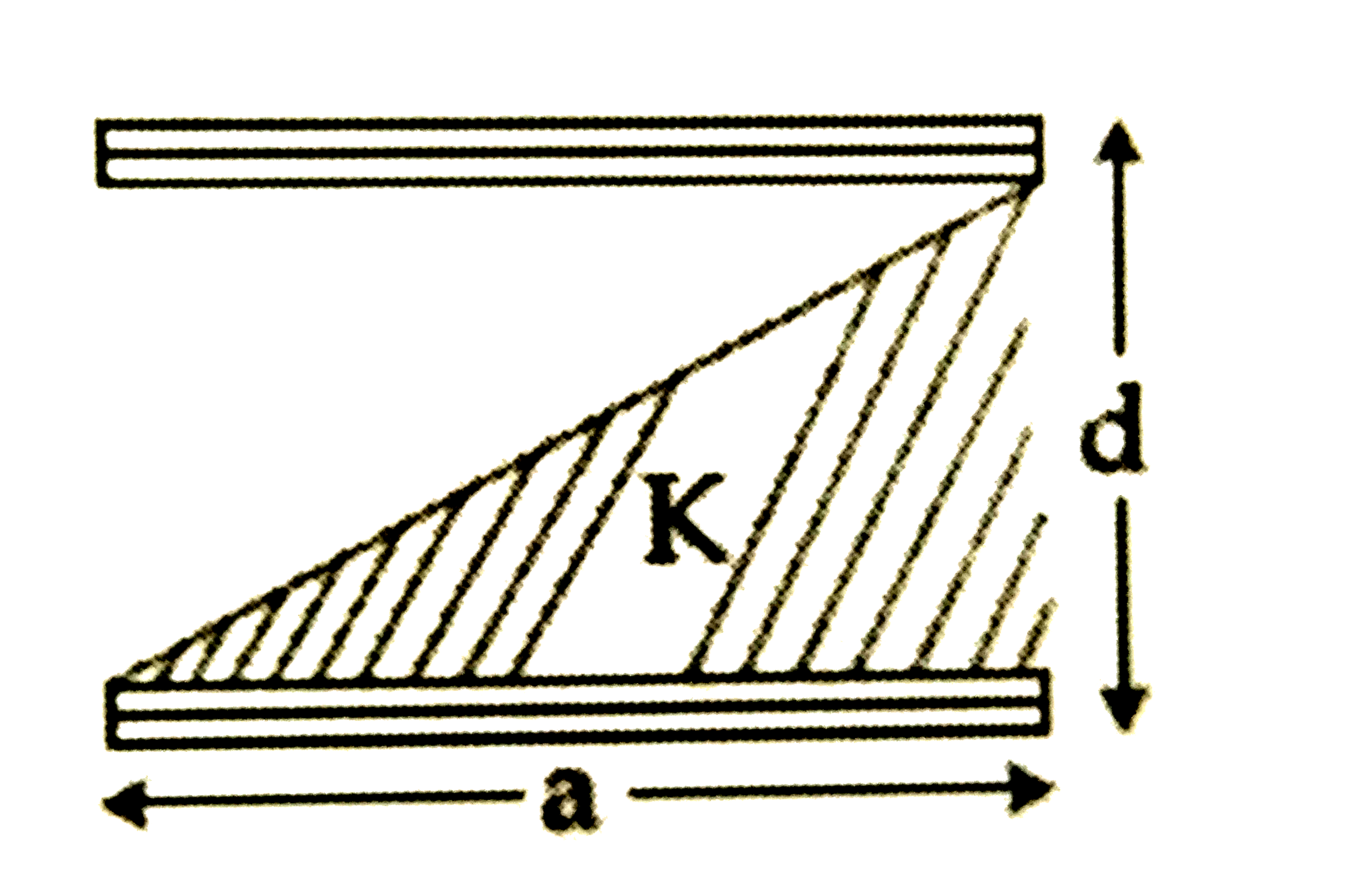
View SolutionA parallel plate capacitor is made of two square plates of side 'a' , separated by a distance d much less than a. The lower triangular portion is filled with a dielectric of dielectric constant K, as shown in the figure. Capacitance of this Capacitor is :
 a) K∈0a22d(K+1)
b) K∈0a2d(K−1)InK
c) K∈0a2dInK
d) 12K∈0a2d
a) K∈0a22d(K+1)
b) K∈0a2d(K−1)InK
c) K∈0a2dInK
d) 12K∈0a2d
View SolutionThe gap between the plates of a parallel plate capacitor having square plate of edge a and plate separation d is filled with a dielectric of dielectric constant K .K varies parallel to an edge as K=K0−ax where k and a are positive constants and x is the distance from one end.The value of alpha for which capacitor behaves as a capacitor of zero capacitance will be
View SolutionFigure shown a parallel-plate capacitor having square plates of edge a and plate-separation d. The gap between the plates is filled with a dielectric of dielectric constant K which varies parallel to an edge as where K and a are constants and x is the distance from the left end. Calculate the capacitance.

View SolutionFigure shown a parallel-plate capacitor having square plates of edge a and plate-separation d. The gap between the plates is filled with a dielectric of dielectric constant K which varies parallel to an edge as K=K0+αx, where K and α are constants and x is the distance from the left end. Calculate the capacitance.

View Solution
