कथन-1 x≥−1 के लिए माना f(x)=(x+1)2 है। यदि g(x) एक फलन है जिसका वक्र रेखा y=x के सापेक्ष फलन f(x) के वक्र का प्रतिबिंब है तब g(x)=√x−1,x≥0,
कथन-2 g(x),f(x) का प्रतिलोम है।
कथन -1 सही है कथन -2 सही है कथन -1 के लिए, कथन -2 का स्पष्टीकरण सही है
कथन-1 सही है कथन -2 सही है: कथन-1 के लिए , कथन -2 का स्पष्टीकरण सही नहीं है
कथन-1 सही है, कथन -2 गलत है
कथन-1 गलत है : कथन-2 सही है
The correct Answer is:A
Step by step video, text & image solution for कथन-1 x ge-1 के लिए माना f(x)=(x+1)^(2) है। यदि g(x) एक फलन है जिसका वक्र रेखा y=x के सापेक्ष फलन f(x) के वक्र का प्रतिबिंब है तब g(x)=sqrt(x)-1,xge0, कथन-2 g(x),f(x) का प्रतिलोम है। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - फलन, सीमा, सांतत्य तथा अवकलनीयताEXERCISE - JEE ADVANCED( MATCH THE COLUMN TYPE)13videos
फलन, सीमा, सांतत्य तथा अवकलनीयता
- BOOK - ERRORLESS HINDICHAPTER - फलन, सीमा, सांतत्य तथा अवकलनीयताEXERCISE - JEE ADVANCED( PASSAGE TYPE)9videos
फलन, सीमा, सांतत्य तथा अवकलनीयता
- BOOK - ERRORLESS HINDICHAPTER - प्रायिकताEXERCISE - EXERCISE99videos
प्रायिकता
- BOOK - ERRORLESS HINDICHAPTER - लघुगणक और आंशिक भिन्नें EXERCISE - JEE Advanced (integer type questions)8videos
लघुगणक और आंशिक भिन्नें
Similar Questions
कॉलम I में दिए गए वक्तव्यों/व्यंजकों का कॉलम II में दिये गये मानों से सुमेल करे।
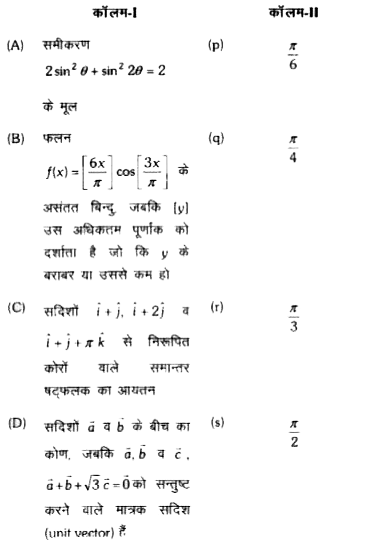 03:05View Solution
03:05View Solutionकथन-1 प्रत्येक फलन, एक सम फलन तथा एक विषम फलन के योग के रूप में अद्वितीय परिभाषित किया जा सकता है।
कथन-2 प्राचल a के मानों का समुच्चय [9,∞) है जिसके लिए फलन f(x) को f(x)=tan(sinx)+[x2a] के द्वारा समुच्चय [−3,3] में एक विषम फलन परिभाषित किया जाता है।05:38View SolutionA, B, C तीन परस्पर स्वतंत्र घटनायें हैं। S1 तथा S2 दो कथनों को देखने पर
S1 : A तथा B∪C स्वतन्त्र हैं
S2 : A तथा B∩C स्वतन्त्र हैं तब05:10View Solutionपद 6+log32⎛⎜ ⎜⎝13√2 ⎷4−13√2 ⎷4−13√2√4−13√2…⎞⎟ ⎟⎠ का मान है
03:20View Solutionफलन f(x)=2sinx का आयाम है -
04:13View Solutionवक्र y=logx,x− अक्ष और x = 2 के बीच का क्षेत्रफल है :
02:46View Solutionx के किन मानों के लिए फलन f(x)=x1+x2 वर्धमान तथा ह्रासमान है।
02:04View Solutionवह अन्तराल ज्ञात कीजिए जिसमें फलन f(x)=x−2x+1 एक वर्धमान फलन है।
04:40View Solutionफलन का x के सापेक्ष समाकलन कीजिए-
x3x2+x+105:53View Solutionx के किन मानो के लिए फलन f(x)=(x)(x2+1 वर्धमान तथा हस्यमान है ?
02:49View Solutionसिद्ध कीजिये की फलन f(x)=tan−1x−x,x∈R के लिए फलां हस्यमान है।
04:51View Solutionफलन y=f(x) के लिए यदि dydx=6(x−2)(x−3) है तो के ty अधिकतम मान के लिए का x मान ज्ञात कीजिये
04:41View Solutionयदि x एक धनात्मक पूर्णाक है, तब Δ=∣∣ ∣ ∣∣x!(x+1)!(x+2)!(x+1)!(x+2)!(x+3)!(x+2)!(x+3)!(x+4)!∣∣ ∣ ∣∣ का मान है-
01:27View Solutionयदि x∈(0,14) के लिए tan−1(6x√x1−9x3) का अवकलन √x.g(x) है, तो g(x) बराबर है
03:35View Solutionयदि f(x)=xयदिx परिमेय है 0यदिx अपरिमेय है तथा g(x)=0यदिx परिमेय हैx यदिx अपरिमेय है तबf−g है
04:50View Solutiona का वह मान जिसके लिए फलन f(x)=√3sinx−cosx−2ax+b सभी x के लिए ह्रासमान है, होगा
04:11View Solution

