A rope thrown over a pulley has ladder (of mass M - m) with a man of mass m on one of its ends and a counterbalancing mass M on its other end The man climbs with a velocity vr relative to a ladder. Pulley and rope are ideal. The velocity of centre of mass of the system is
mMvr
m2Mvr
Mmvr
2Mmvr
The correct Answer is:B
Topper's Solved these Questions
- CENTRE OF MASSBOOK - AAKASH SERIESCHAPTER - CENTRE OF MASSEXERCISE - PRACTICE SHEET (EXERCISE - II) LEVEL - I
2 Videos
- CENTRE OF MASSBOOK - AAKASH SERIESCHAPTER - CENTRE OF MASSEXERCISE - PRACTICE SHEET (EXERCISE - III) LEVEL - I
3 Videos
- CENTRE OF MASSBOOK - AAKASH SERIESCHAPTER - CENTRE OF MASSEXERCISE - PRACTICE SHEET (EXERCISE - I) LEVEL - I
7 Videos
- CALORIMETRY BOOK - AAKASH SERIESCHAPTER - CALORIMETRY EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) (LECTURE SHEET (ADVANCED)(Matrix Type Questions)
1 Videos
- COLLISIONS BOOK - AAKASH SERIESCHAPTER - COLLISIONS EXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
4 Videos
Similar Questions
A rope thrown over a pulley has a ladder with a man of mass m on one of its ends and a counter balancing mass M on its other end. The man climbs with a velocity vr relative to ladder. Ignoring the masses of the pulley and the rope as well as the friction on the pulley axis, the velocity of the centre of mass of this system is:
View SolutionA rope thrown over a pulley has a on one of its ends and a counterbalancing mass M on its other end. The man whose mass is m, climbs upwards by →△r relative to the ladder and then stops. Ignoring masses of the pulley and the rope, as well as the friction the pulley axis, find the displacement of the centre of mass of this system.
View Solution
Knowledge Check
A rope thrown over a pulley has a ladder with a man of mass m on one of its ends and a counter balancing mass M on its other end. The man climbs with a velocity vr relative to ladder. Ignoring the masses of the pulley and the rope as well as the friction on the pulley axis, the velocity of the centre of mass of this system is:
AmMvrBm2MvrCMmvrD2Mmvr
A rope thrown over a pulley has a on one of its ends and a counterbalancing mass M on its other end. The man whose mass is m, climbs upwards by →△r relative to the ladder and then stops. Ignoring masses of the pulley and the rope, as well as the friction the pulley axis, find the displacement of the centre of mass of this system.
View SolutionA man of mass m is suspended in air by holding the rope of a ballon of mass M. As the man climbs up the rope, the ballon
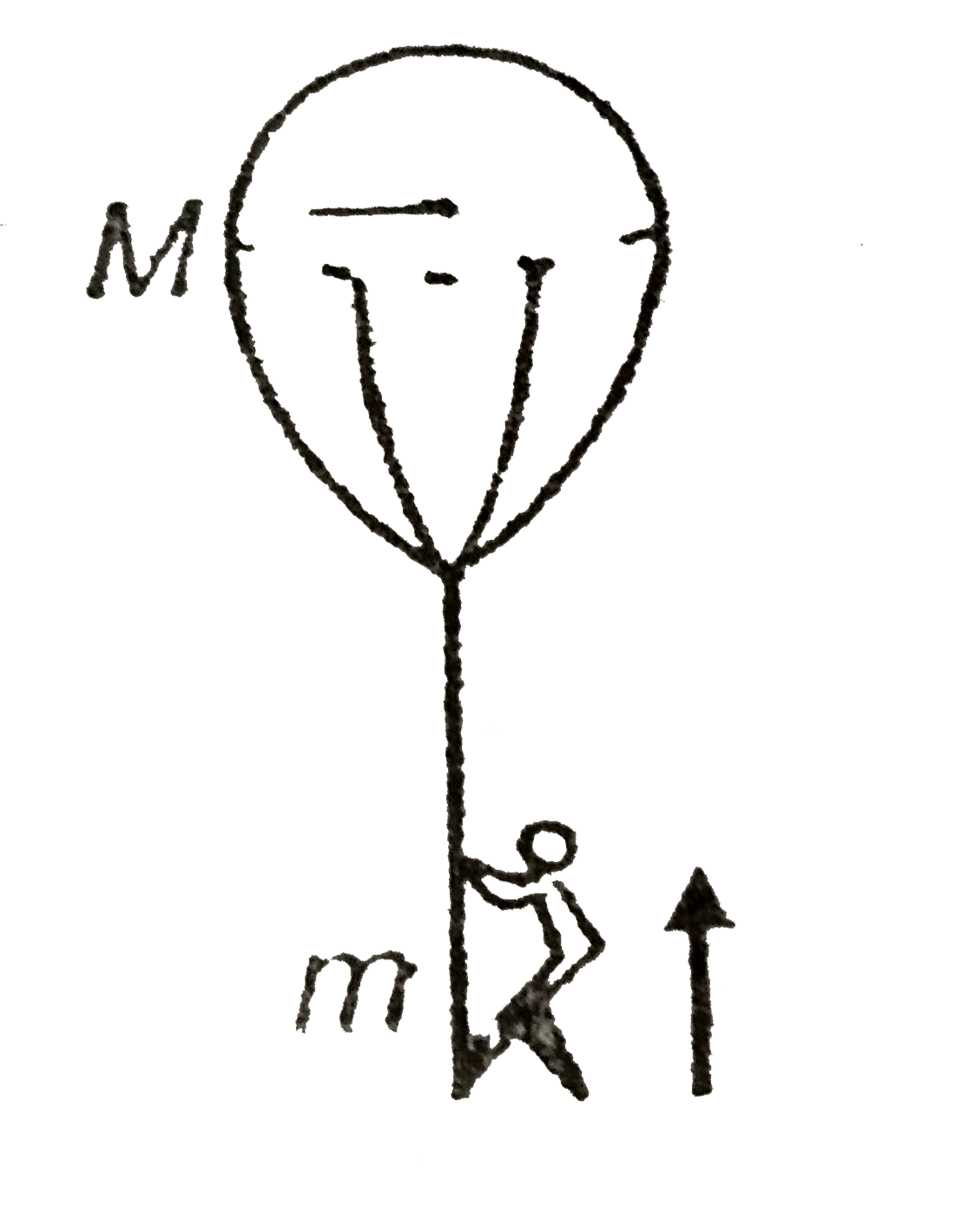
View SolutionA man of mass m is suspended in air by holding the rope of a ballon of mass M. As the man climbs up the rope, the ballon
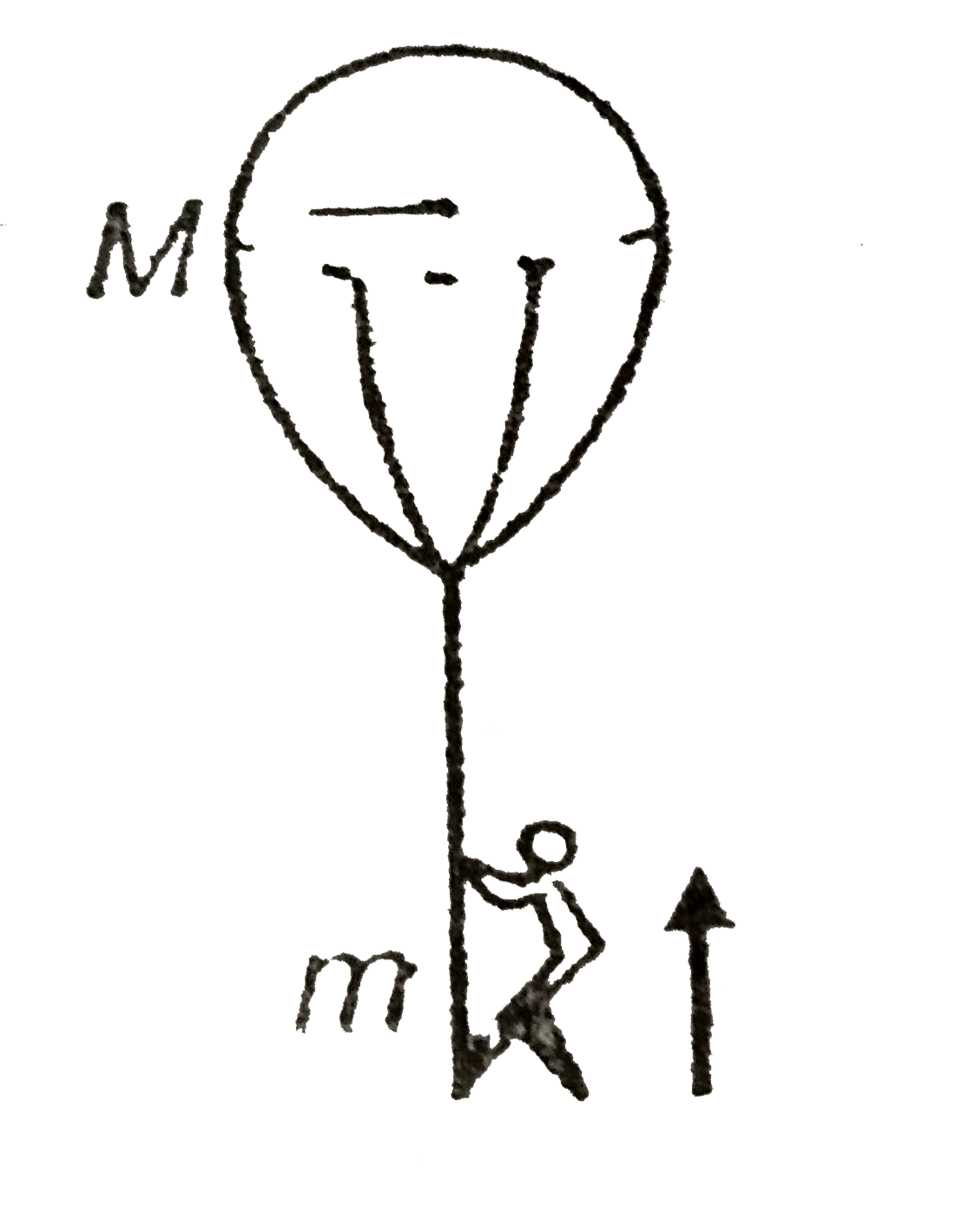
View SolutionA man of mass m is suspended in air by holding the rope of a ballon of mass M. As the man climbs up the rope, the ballon
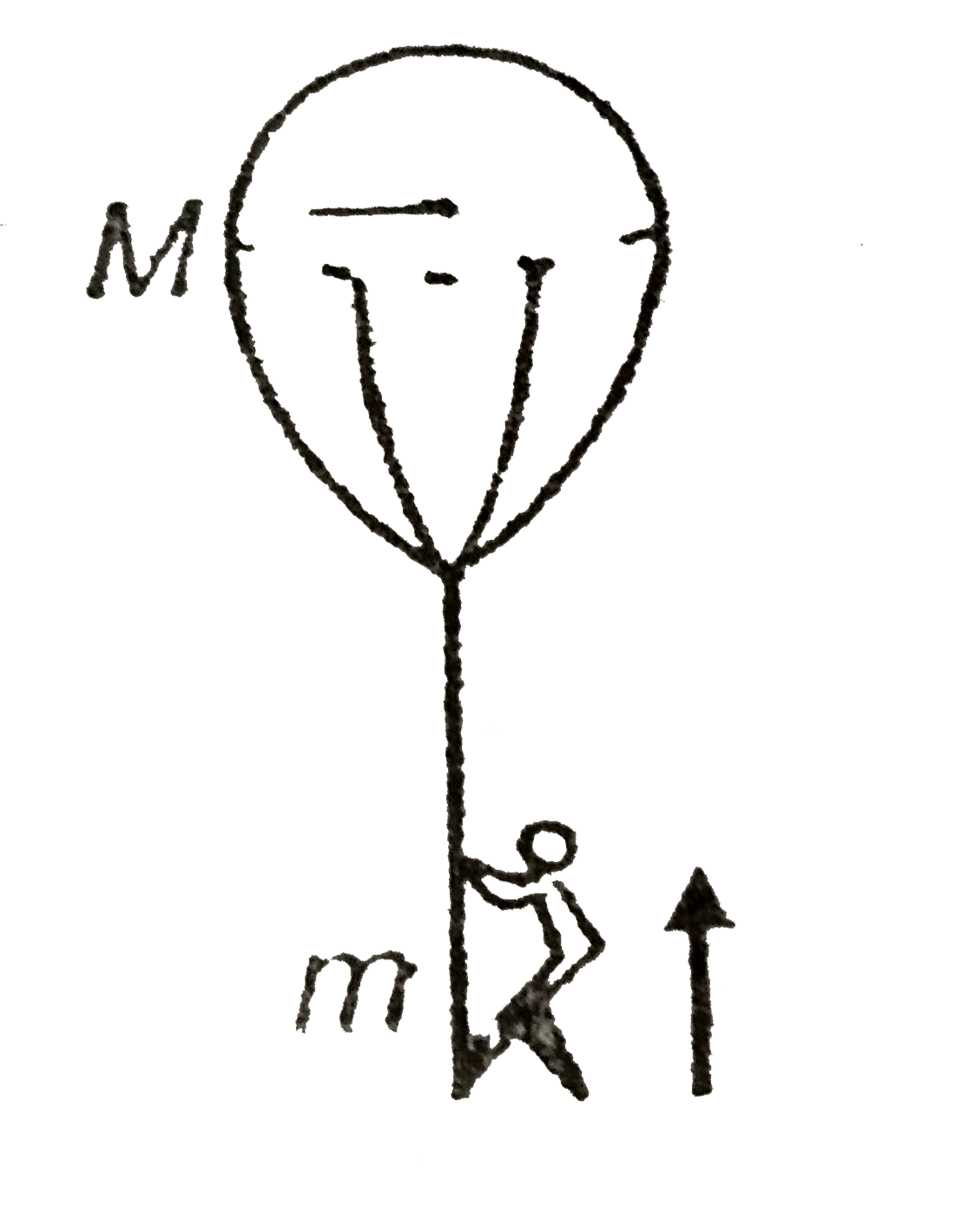
View SolutionA balloon of mass M is stationary in air. It has a ladder on which a man of mass m is standing. If the man starts climbing up the ladder with a velocity of relative to ladder, the velocity of balloon is
View SolutionTwo ladders are hanging from ands of a light rope passing over a light and smooth pulley. A monkey of mass 2m hangs near the bottom of one ladder whose mass is M-2m. Another monkey of mass m hangs near the bottom of the other ladder whose mass is M-m. The monkey of mass 2m moves up a distance l with respect to the ladder. The monkey of mass m moves up a distance l/2 with respect to the ladder. The displacement of centre of mass of the system is kml4M. Find the value of k.

View SolutionTwo ladders are hanging from ands of a light rope passing over a light and smooth pulley. A monkey of mass 2m hangs near the bottom of one ladder whose mass is M-2m. Another monkey of mass m hangs near the bottom of the other ladder whose mass is M-m. The monkey of mass 2m moves up a distance l with respect to the ladder. The monkey of mass m moves up a distance l/2 with respect to the ladder. The displacement of centre of mass of the system is kml4M. Find the value of k.

View Solution
