A rope thrown over a pulley has a on one of its ends and a counterbalancing mass M on its other end. The man whose mass is m, climbs upwards by →△r relative to the ladder and then stops. Ignoring masses of the pulley and the rope, as well as the friction the pulley axis, find the displacement of the centre of mass of this system.
Let displacement of counterweight be △y therefore the dispacement of ladder will be (−△y).
Displacement of man △ym=△ym,l+△yl
Ymj= displancement of man w.r.t of ladder =△→r
ym=(△r−△y)
Hence displacement of centre of mass of the system
△→rc=Mmass△→rmassMladder+△→rladder+Mmean△→rmanMmass+Mladder+Mman
△rc=M△y+(M−m)−(△y)+m(△r−△y)M+(M−m)+m
⇒△rc=m△r2m(upward)
Method 2: All the bodies of the system are initially at rest. The rope tension is the same both as on the left and the right hand side, at every instant and consequently the momenta of the counterbalancing mass (→p1) and the ladder with the Man (→p2) are equal at any moment of time. i.e.,

→p1=→p2
or M→v1=m→v+(M−M)→v1............i
Here →v1 and →v are the velocities of the mass and the man respectively.
Velocity of man →vman→vman, ladder+→vladder=v'−v1...........ii
Where →v' is the man's velocity relative of the ladder.
From eqn i and ii we obtain →v1=(m2M)→v'
on the other hand the momentum of the centre of mass is
→p=→p1+→p2=2→p1
or 2M→vC=2M.→v1 or →vC=→v1=(m2m)→v'
are finally the desired displacement is
△→rC=∫→vC.dt=m2m∫→v'dt=m2M△→r
or displacement of centre of mass of system is
△→rC=m2M△→r As system I and system II both are having same mass and experiene equal force. Both starts from rest. hence displacement of centre of masses fo systems should be equal. As the system I has only one object, the diaplacement of the object will be same as the displascement of its centre of mass which is △y upward. hence the displacement of centre of mass of system II will so be △y upward
(△→ycm)systemI=(△→ycm)systemII=△y(upward)
⇒△y=m(△r−△y)+(M−m)(−△y)m(M−m)
⇒△y=m△r2M(upward)

Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.1
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.2
23 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A rope thrown over a pulley has a ladder with a man of mass m on one of its ends and a counter balancing mass M on its other end. The man climbs with a velocity vr relative to ladder. Ignoring the masses of the pulley and the rope as well as the friction on the pulley axis, the velocity of the centre of mass of this system is:
View SolutionA stationary pulley carries a rope whose one end supports a ladder with a man and the other end the counterweight of mass M. The man of mass m climbs up a distance l with respect to the ladder and then stops. Neglecting the mass of the rope and the friction in the pulley axle, find the displacement I of the centre of inertia of this system.
View Solution
Knowledge Check
A rope thrown over a pulley has a ladder with a man of mass m on one of its ends and a counter balancing mass M on its other end. The man climbs with a velocity vr relative to ladder. Ignoring the masses of the pulley and the rope as well as the friction on the pulley axis, the velocity of the centre of mass of this system is:
AmMvrBm2MvrCMmvrD2MmvrA stationary pulley carries a rope whose one end supports a ladder with a man and the other end the counterweight of mass M. The man of mass m climbs up a distance l′ with respect to the ladder and then stops. Neglecting the mass of the rope and the friction in the pulley axle, find the displacement I of the centre of inertia of this system.
AmlM+mBml2MCmlM+2mDml2M+m
A stationary pulley carries a rope whose one end supports a ladder with a man and the other end the counterweight of mass M. The man of mass m climbs up a distance I′ with respect to the ladder and then stops. Neglecting the mass of the rope and the friction in the pulley axle, find the displacement I of the centre of inertia of this system.
View SolutionA pulley fixed to the ceiling carried a thread with bodies of masses m1 and m2 attached to its ends. The mases of the pulley and the thread are negligible and friction is absent. Find the acceleration of the centre of mass of this system.
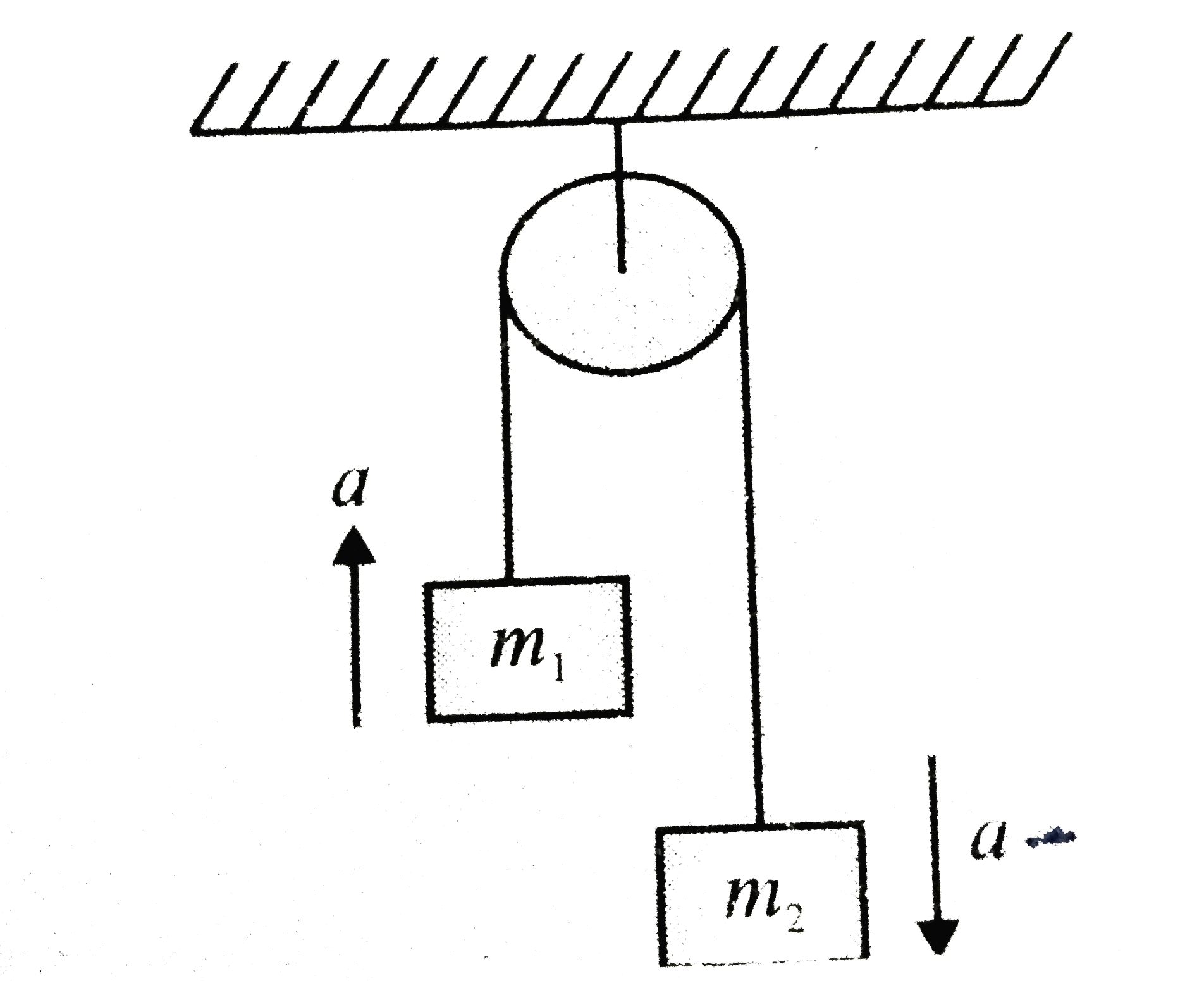
View SolutionA pulley fixed to the ceiling carried a thread with bodies of masses m1 and m2 attached to its ends. The mases of the pulley and the thread are negligible and friction is absent. Find the acceleration of the centre of mass of this system.
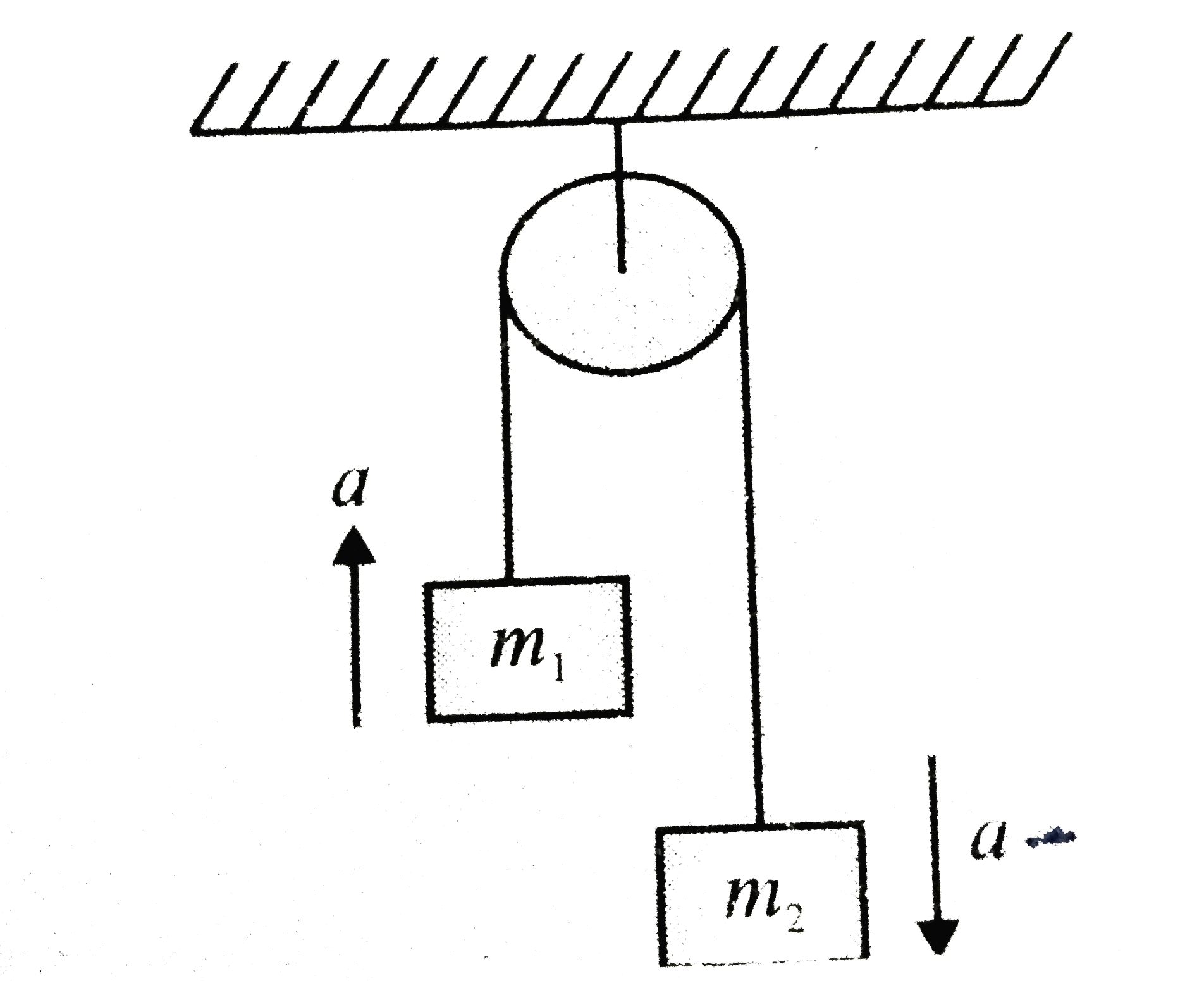
View SolutionA pulley fixed to the ceiling carries a thread with bodies of masses m1 and m2 attached at its ends. The masses of the pulley and thread are negligible, friction is absent. Find the acceleration of the centre of mass(acm) of this system.
View SolutionA pulley fixed to the ceiling carries a thread with bodies of masses m1 and m2 attached to its ends. The masses of the pulley and the thread are negligible, friction is absent. Find the acceleration wC of the centre of inertia of this system.
View SolutionTwo ladders are hanging from ands of a light rope passing over a light and smooth pulley. A monkey of mass 2m hangs near the bottom of one ladder whose mass is M-2m. Another monkey of mass m hangs near the bottom of the other ladder whose mass is M-m. The monkey of mass 2m moves up a distance l with respect to the ladder. The monkey of mass m moves up a distance l/2 with respect to the ladder. The displacement of centre of mass of the system is kml4M. Find the value of k.

View Solution
