A uniform circular sheet has a radius r. A square sheet whose diagonal length is equal to radius of the plate is removed. The maximum distance of the centre of mass of the remaining plate from the centre of this original sheet is
r2(2π−1)
r(π−2)
2rπ−3
r2(π−1)
The correct Answer is:A
Topper's Solved these Questions
- CENTRE OF MASSBOOK - AAKASH SERIESCHAPTER - CENTRE OF MASSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) LECTURE SHEET (ADVANCED)
9 Videos
- CENTRE OF MASSBOOK - AAKASH SERIESCHAPTER - CENTRE OF MASSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED))
3 Videos
- CENTRE OF MASSBOOK - AAKASH SERIESCHAPTER - CENTRE OF MASSEXERCISE - PRACTICE SHEET (EXERCISE - III) LEVEL - I
3 Videos
- CALORIMETRY BOOK - AAKASH SERIESCHAPTER - CALORIMETRY EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) (LECTURE SHEET (ADVANCED)(Matrix Type Questions)
1 Videos
- COLLISIONS BOOK - AAKASH SERIESCHAPTER - COLLISIONS EXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
4 Videos
Similar Questions
A circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
View SolutionFrom a uniform circular disc of mass M and radius R a small circular disc of radius R/2 is removed in such a way that both have a common tangent. Find the distance of centre of mass of remaining part from the centre of original disc.
View Solution
Knowledge Check
Figure shows a square plate of uniform thickness and side length √2m. One fourth of the plate is removed as indicated. The distance of centre of mass of the remaining portion from the centre of the original square plate is
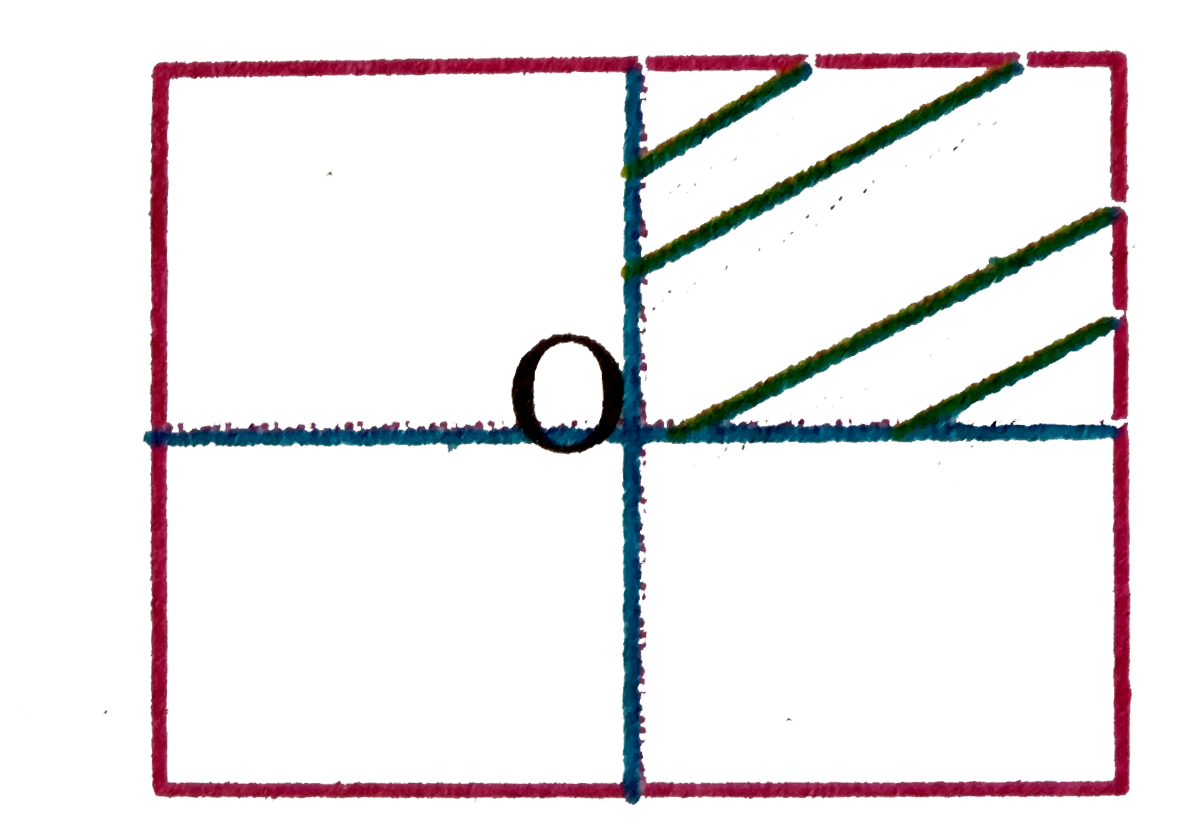 A1/3mB1/2mC1/6mD1/8m
A1/3mB1/2mC1/6mD1/8mA circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
A3/35 cmB1/35 cmC3/10 cmD7/35 cmA uniform sphere has radius R. A sphere of diameter R is cut from its edge as shown. Then the distance of centre of mass of remaining portion from the centre of mass of the original sphere is
 AR/7BR/14C2R/7DR/18
AR/7BR/14C2R/7DR/18
From a uniform circular disc of mass M and radius R a small circular disc of radius R/2 is removed in such a way that both have a common tangent. Find the distance of centre of mass of remaining part from the centre of original disc.
View SolutionFrom a uniform square plate, one-fourth part is removed as shown. The centre of mass of remaining part will lie on
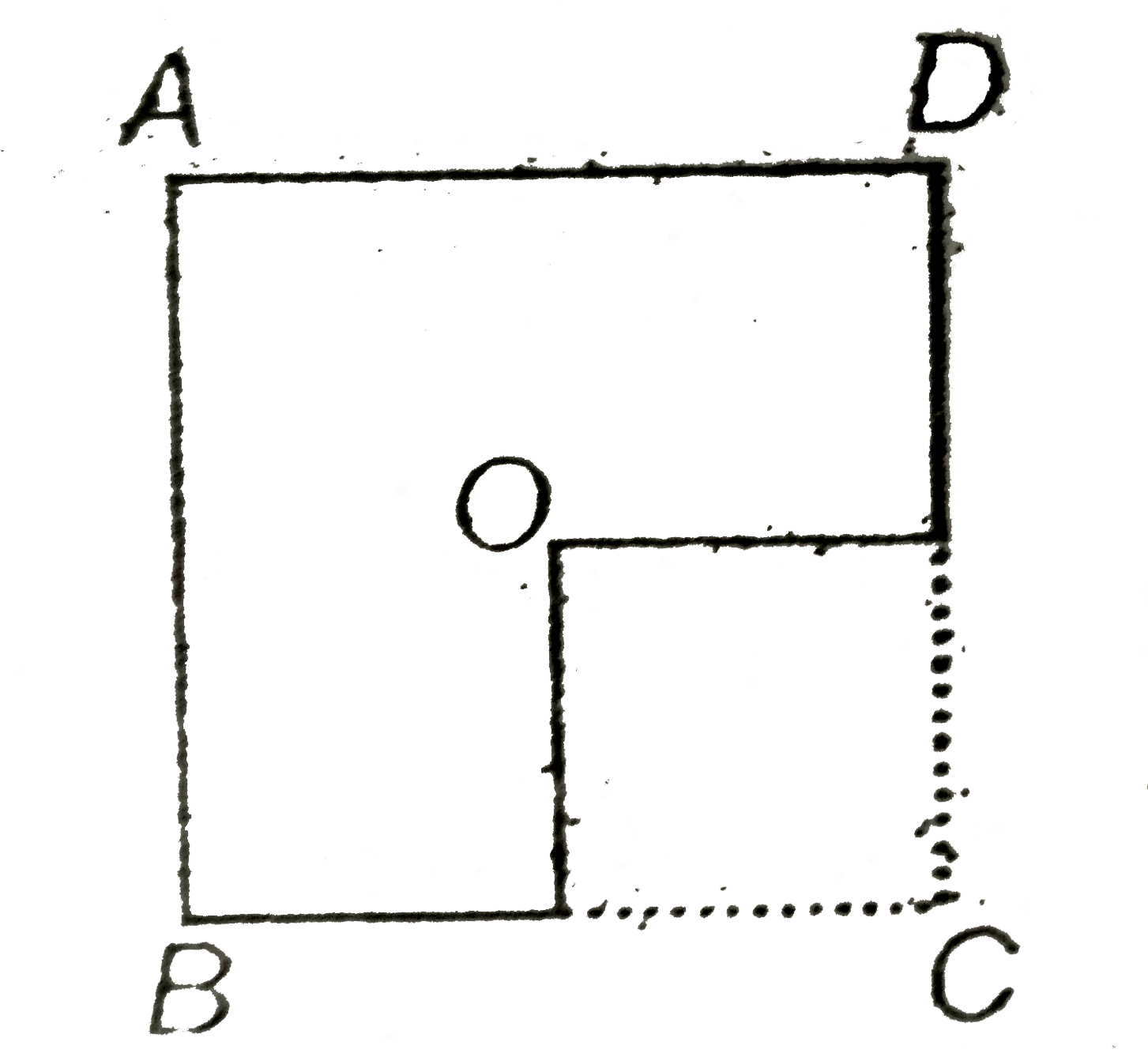
View SolutionFrom a uniform square plate, one-fourth part is removed as shown. The centre of mass of remaining part will lie on

View SolutionFrom a uniform square plate, one-fourth part is removed as shown. The centre of mass of remaining part will lie on

View SolutionA circular hole of radius r is made in a disk of radius R and of uniform thickness at a distance a from the centre of the disk. The distance of the new centre of mass from the original centre of mass is
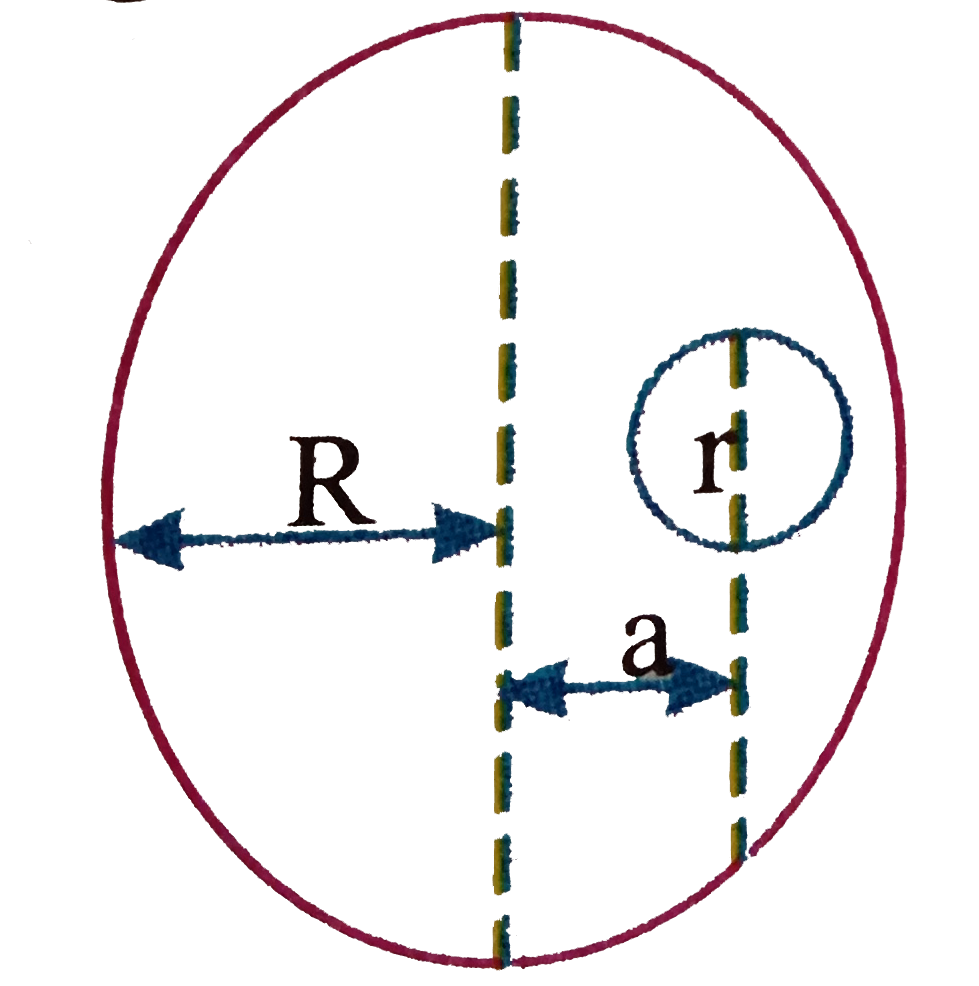
View Solution
