A uniform thin rod of length 50 cm is bent so as to form the five sides of a regular hexagon. The distance of centre of mass from either end is
√13/4cm
√133cm
√22cm
10 cm
The correct Answer is:B
Topper's Solved these Questions
- CENTRE OF MASSBOOK - AAKASH SERIESCHAPTER - CENTRE OF MASSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) LECTURE SHEET (ADVANCED)
9 Videos
- CENTRE OF MASSBOOK - AAKASH SERIESCHAPTER - CENTRE OF MASSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED))
3 Videos
- CENTRE OF MASSBOOK - AAKASH SERIESCHAPTER - CENTRE OF MASSEXERCISE - PRACTICE SHEET (EXERCISE - III) LEVEL - I
3 Videos
- CALORIMETRY BOOK - AAKASH SERIESCHAPTER - CALORIMETRY EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) (LECTURE SHEET (ADVANCED)(Matrix Type Questions)
1 Videos
- COLLISIONS BOOK - AAKASH SERIESCHAPTER - COLLISIONS EXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
4 Videos
Similar Questions
Knowledge Check
A thin uniform rod of length L is bent at its mid point as shown in the figure. The distance of the centre of mass from the point O is
 AL2sin(θ2)BL2cos(θ2)CL4sin(θ2)DL4cos(θ2)
AL2sin(θ2)BL2cos(θ2)CL4sin(θ2)DL4cos(θ2)A uniform wire of length l is bent into the shape of 'V' as shown. The distance of its centre of mass from the vertex A is :-
 Al/2Bl√34Cl√38DNone of these
Al/2Bl√34Cl√38DNone of theseA uniform metal rod of length 1m is bent at 90∘, so as to form two arms of equal length. The centre of mass of this bent rod is
Aon the bisector of the angle, (1√2) m from vertexBon the bisector of angle, (12√2) m from vertexCon the bisector of the angle, (12) m from vertexDon the bisector of the angle, (14√2)m from vertex
Two uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

View SolutionA thin uniform wire is bent to form the two equal sides AB and AC of triangle ABC, where AB=AC=5 cm. The third side BC, of length 6cm, is made from uniform wire of twice the density of the first. The distance of centre of mass from A is :
View SolutionA uniform rod o length one meter is bent at its midpoint to make 90∘. The distance of centre of mass from the centre of rod is (in cm)
View SolutionTwo identical thin uniform rods of length L each are joined to form T shape as shown in the figure. The distance of centre of mass from D is
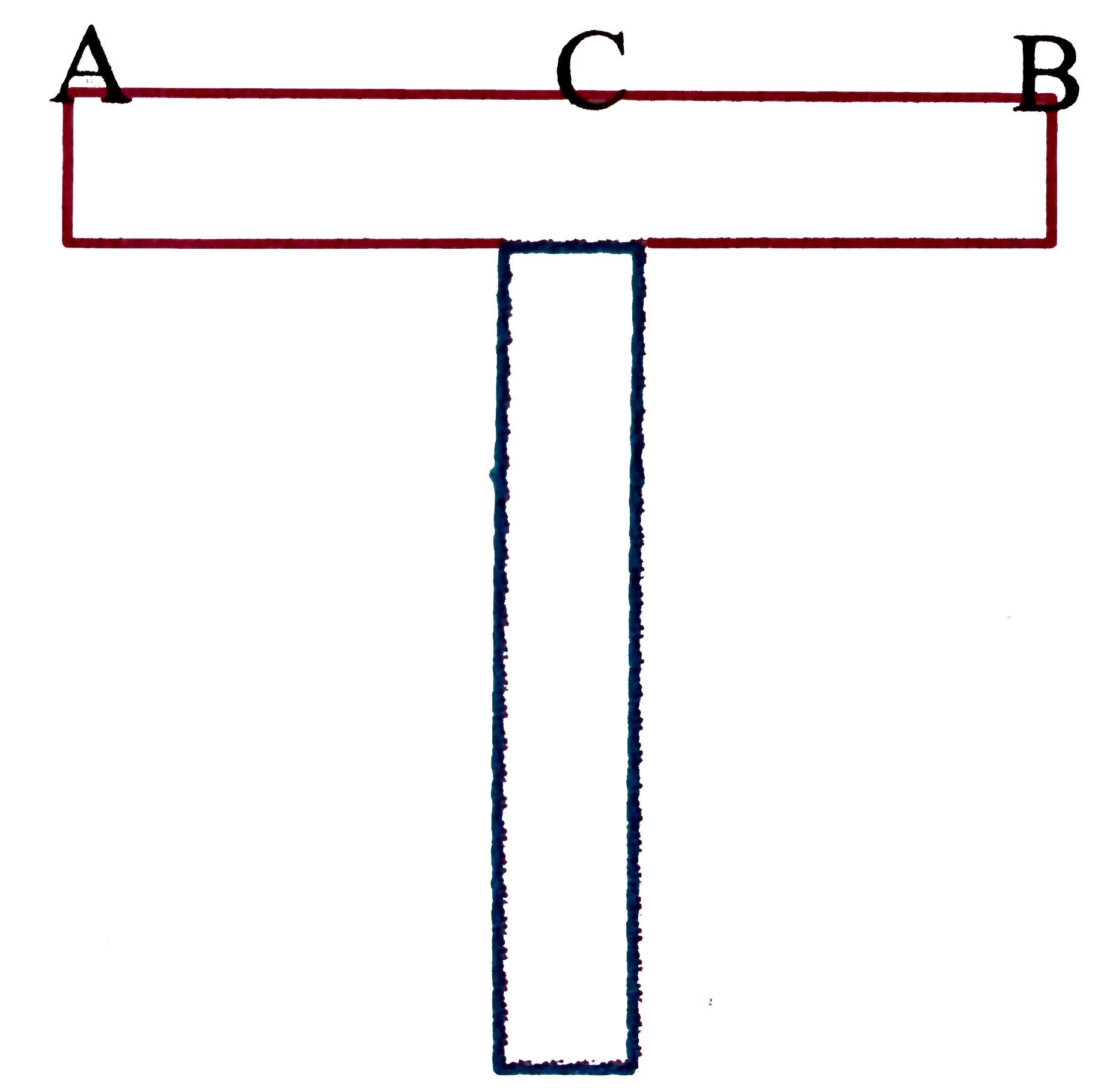
View SolutionA thin uniform wire is bent to form the two equal sides AB and AC of triangle ABC, where AB=AC=5 cm. The third side BC, of length 6cm, is made from uniform wire of twice the density of the first. The distance of centre of mass from A is :
View Solution

