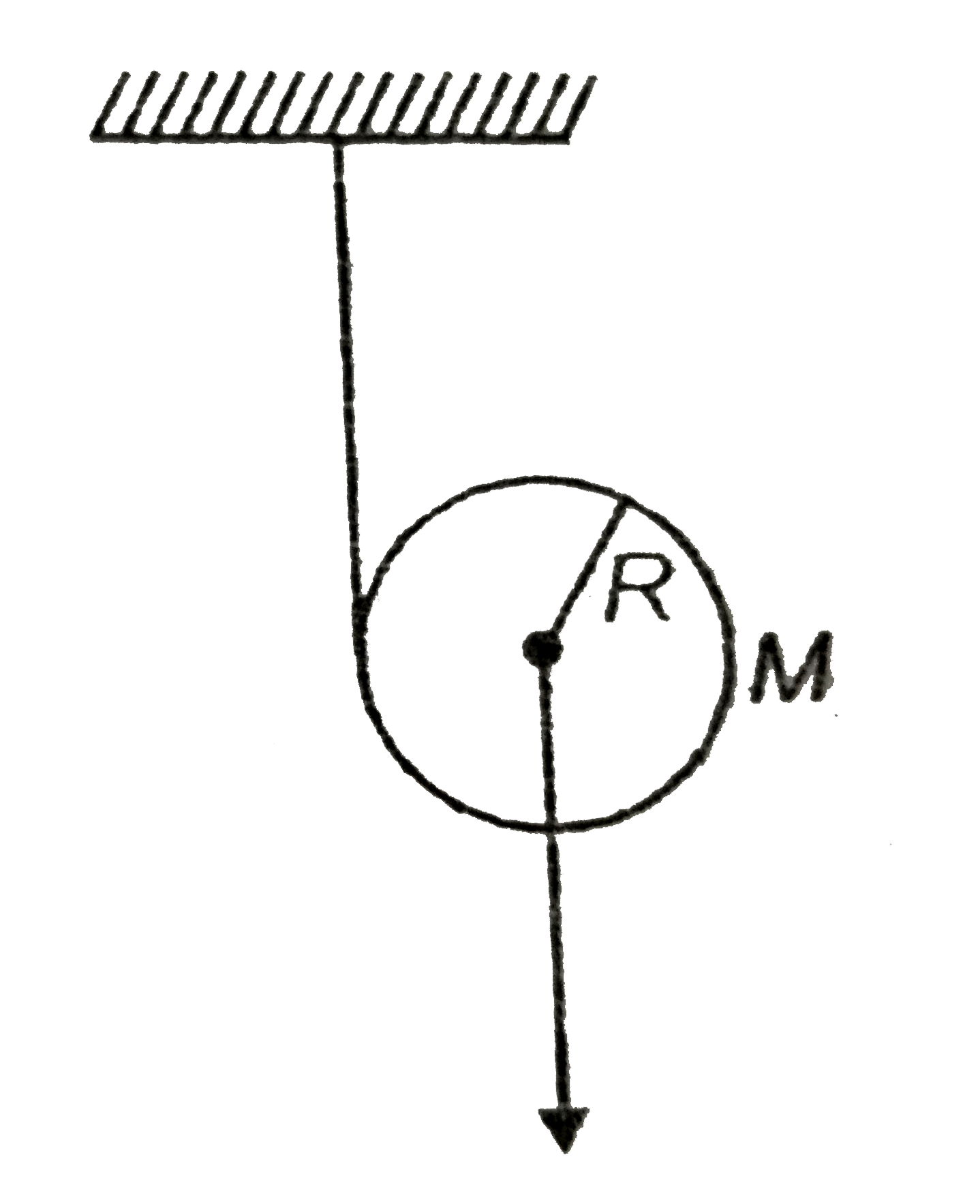
A string is wound around a disc of radius r and mass M and at the free end of the string a body of mass m is suspended. The body is then allowed to descend. Show that the angular accelerationof the disc = $\frac{m g}{R (M + \frac{m}{2})}$ Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

The suspended body and the forces acting on the disc are shown in fig.
The equation of the linear motion of the suspended body is $m a = m g - T$
(where T = tension in the string)
$∴ T = m (g - a)$
Now torque acting on disc $τ = R T [∵ \vec{τ} = \vec{r} \times \vec{F}]$
$∴ I α = R T$
$∴ α = \frac{R T}{I} = \frac{R m (g - a)}{I}$
$∴ α = \frac{R m (g - a)}{M \frac{R^{2}}{2}} [∵ I = \frac{M R^{2}}{2}]$
$∴ α = \frac{2 m}{R M} (g - a) but a = R α$
$∴ α = \frac{2 m g}{R M} - \frac{2 m R α}{R M}$
$∴ α + \frac{2 m R α}{R M} = \frac{2 m g}{R M}$
$∴ α (1 + \frac{2 m}{M}) = \frac{2 m g}{R M}$
$∴ α = \frac{2 m g}{R M (1 + \frac{2 m}{M})} = \frac{m g}{\frac{R}{2} (M + \frac{2 m M}{M})} = \frac{m g}{R (\frac{M}{2} + m)}$

Updated on:21/07/2023

|

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

KUMAR PRAKASHAN-SYSTEMS OF PARTICLES AND ROTATIONAL MOTION-SECTION-B NUMERICAL FROM .DARPAN. BASED ON TEXTBOOK

Home
Ask Doubt
Profile