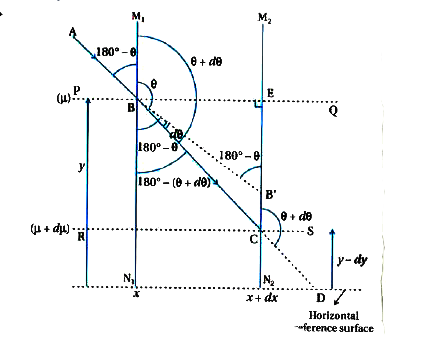
The mixture a pure liquid and a solution in long vertical column (i.e, horizontal dimensions vertical dimensions ) Produce diffusion of solute particles and hence refractive index gradient along the vertical dimesion . A ray of light entering the column I at right angles to the vertical is deviated from its original path. Find the deviated from its original path. Find the deviation in travelling a horizontal distance h, the height of the coloumn.
 Solution in Gujrati
Solution in Gujrati
As shown in the figure, consider an extremely narrow region of width dx, between the layers at distances x and x + dx , inside the extremely high cylindrical column of liquid .
In above region, point B is on the level , at height y from horizontal reference level, where refractive index is and gradient of refractive index. is . At this point, light ray is incident at angle
, makes angle with normal drawn on horizontal surface , which becomes angle of incidence. ) If there would not be any gradient of refractive index, ray would have come to point B.. But here refractive index increases with the decreases in height and so at level height is (y - dy) and refractive indes is which is more than . Hence, ray bends towards normal and so it advances from B to C. Thus, ray becomes refracted light ray which makes angle with normal . Now applying Snell.s law at point B ion above figure, we get,
Since is extremely small, we can take sin
are negligible)
.........(1)
For the right angled BEB. in the figure
..........(2)
From equation (1) and (2,)
Taking integration on both the sides,
During horizontal displacement remain constant)
d
Above equation gives required result .
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - KUMAR PRAKASHANCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - SECTION-D (MULTIPLE CHOICE QUESTIONS (MCQs))(MCQs FROM .DARPAN. BASED ON TEXTBOOK)
26 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - KUMAR PRAKASHANCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - SECTION-D (MULTIPLE CHOICE QUESTIONS (MCQs))(MCQs FROM .DARPAN. BASED ON TEXTBOOK)(REFRACTION)
32 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - KUMAR PRAKASHANCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - SECTION-C (NCERT EXEMPLAR SOLUTION) (SHORT ANSWER TYPE QUESITONS)
6 Videos
- MOVING CHARGES AND MAGNETISMBOOK - KUMAR PRAKASHANCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - SECTION D (MCQs ASKED IN COMPETITIVE EXAMS)
34 Videos
- SAMPLE QUESTION PAPER BOOK - KUMAR PRAKASHANCHAPTER - SAMPLE QUESTION PAPER EXERCISE - PART-B SECTION-C
5 Videos
Similar Questions
Diameter of spherical mirror is 10 cm, what will be aperture of mirror ?
View SolutionRefraction index of medium-2 with respect to medium-1 is ...... .
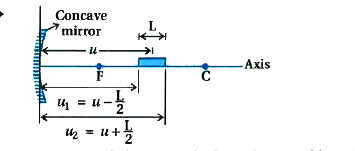
View SolutionA short object of length L is placed along the principal axis of a concave mirror away from focus. The object distance is u. If the mirror has a focal length f, what will be the length of the image ? You may take L<<|v−f|.
View SolutionElectric charge Q having mass M moves on a circular path of radius R with velocity →v, perpendicular to uniform magnetic field B. When a particle completes one revolution, work done by the field is _______
View SolutionTwo charges –q and +q are located at points (0, 0, –a) and (0, 0, a), respectively.
(a) What is the electrostatic potential at the points (0, 0, z) and (x, y, 0) ?
(b) Obtain the dependence of potential on the distance r of a point from the origin when r/a>>1 .
(c) How much work is done in moving a small test charge from the point (5,0,0) to (–7,0,0) along the x-axis? Does the answer change if the path of the test charge between the same points is not along the x-axis?
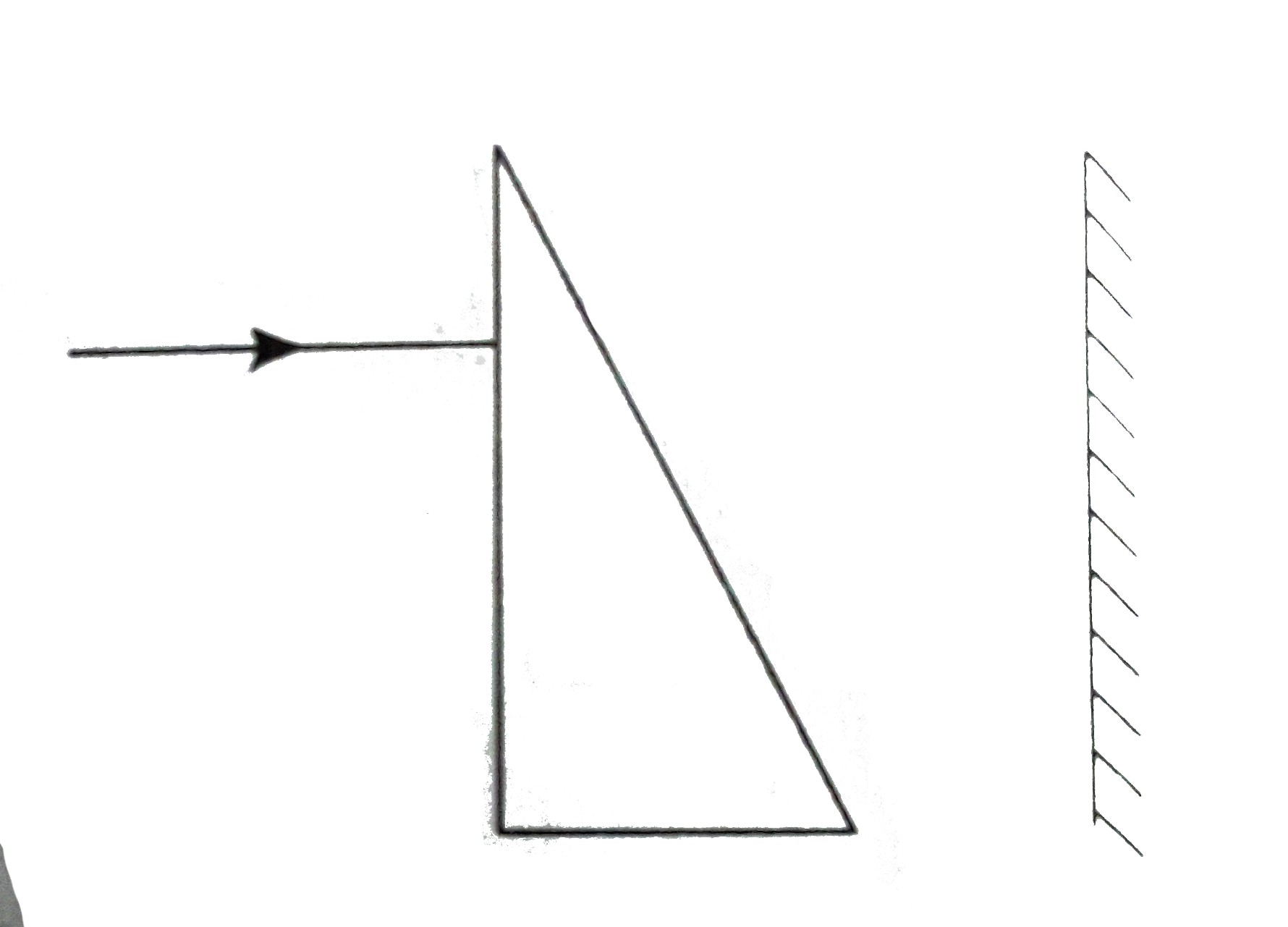
View SolutionA right-angled prism of apex angle 4∘ and refractive index 1.5 is located in front of a vertical plane mirror as shown in figure. A horizontal ray of light is falling on the prism. Find the total deviation produced in the light ray as it emerges 2nd time from the prism.
View SolutionThe mixture of a pure liquid and a solution in a along vertical column (i.e., horizontal dimensions lt lt vertical dimensions) produces diffusion of solute particles and hence a refractive index gradient along the vertical dimension. A ray of light entering the column at right angles to the vertical is deviated from its original path. Find the deviation in travelling a horizontal distance d lt lt h , the height of the column.
View SolutionA light ray incidents on water (n=4/3) surface from air and reflected from air and reflected part of it is found to be polarized. Find the deviation of refracted light from its original path:
View SolutionA force of 4N is inclined at an angle of 60∘ from the vertical. Find out its components along horizontal and vertical directions.

View Solutionयदि प्रकाश-किरण काँच के गुटके पर लंबवत गिरे तो अपवर्तन कोण कितना होगा ? विचलन कोण कितना होगा ?
View Solutionजब प्रकाश की एक किरण एक माध्यम से दूसरे माध्यम में जाती है तो अपने पूर्व पथ से विचलित हो जाती है। इसे कहते है।
View Solutionप्रकाश की एक किरण एक समतल दर्पण पर लंबवत आपतित होती है। दर्पण द्वारा किरण के पथ में उत्पन्न विचलन का मान होगा
View SolutionThe mixture of a pure liquid and a solution in a along vertical column (i.e., horizontal dimensions lt lt vertical dimensions) produces diffusion of solute particles and hence a refractive index gradient along the vertical dimension. A ray of light entering the column at right angles to the vertical is deviated from its original path. Find the deviation in travelling a horizontal distance d lt lt h , the height of the column.
View SolutionThe mixture of a pure liquid and a solution in a along vertical column (i.e., horizontal dimensions << vertical dimensions) produces diffusion of solute particles and hence a refractive index gradient along the vertical dimension. A ray of light entering the column at right angles to the vertical is deviated from its original path. Find the deviation in travelling a horizontal distance d<<h, the height of the column.
View SolutionA long vertical column (ie, horizontal dimensions lt lt A mixture of pure fluid and a solution in the kadhir dimensions) produces diffusion of solute particles and thus a refractive gradient corresponding to vertical dimensions. In this column, the light beam that enters the vertical vertically deviates from its original path. Horizontal distance d lt lt h Find the deviation in walking. Here h is the height of the column.
View Solution
