
Consider a thin lens placed between a source (S) and an observer (O) (see figure) . Let the thicknes of the lens very as w(b)=w0−b2α,
where b is the verticle distance from the pole.
w0 is constant. Using Fermat.s principle i.e. the time of transit for a ray between the source and observer is an extremum, find the condition that all paraxial rays starting from the source will converage at a point O on the axis. Find the focal length.
(ii) A gravitational lens may be assumed to have a varying width of the from
w(b)=k1ln(k2b)bmin<b<bmax
=k1ln(k2bmin)b<bmin
Show that an observe will see an image of a point object as a right about the center of the lens with and angular radius
β=√(n−1)k1uvu+vSolution in Gujrati
⇒ (i) Time taken by light ray to travel from S to P1
t1=SP1c=(u2+b2)1/2c={u2(1+b2u2)}12c
∴t1=uc(1+b2u2)12
⇒ Here b2u2<<1 and so expanding according to binomial theorem and then retaining only first two terms,
t1≈uc(1+b22u2) .......(1)
⇒ Similarly, time taken by light ray to travel from P1 to O,
t2=P1Oc=(v2+b2)12c={v2(1+b2v2)}12c
∴t2=vc(1+b2v2)12
⇒ Here b2b2<<1 and so expanding according to binomial theorem and then rataining only first two terms ,
t2=vc(1+b22v2).......(2)
⇒ Now time taken by light ray to travel trough thickness W of a lens at point P1
t2=vc(1+b22v2)
⇒ Now time taken by light ray to travel trough thickness W of a lesns at point P1
t3=(n−1)Wc
(As per statement W=W0−b2α)......(3)
⇒ Now, total time taken by light ray to travel from S to P1 to O is t then,
t=t1+t2+t3
∴t=uc(1+b22b2)+vc(1+b22v2)+(n−1)Wc
∴t=1c(u+b22u)+1c(v+b22v)+1c(n−1)W
∴t1c[u+v+b22(1u+1v)+(n−1)W]
⇒ Here, for the sake of simplicity, if we assume
1u+1v=1D then ......(4)
t=1c[u+v+b22D+(n−1)W].....(5)
∴t=1c[u+v+b22D+(n−1)(w0−b2α)]....(6)
As per statement
∴dtdb=1c[0+0+12(2b)+(n−1)(0−1α×2b)]
∴dtdb=1c[bD−2bα(n−1)]........(7)
⇒ Now , according to Farmar.s principle above time t is either maximum or mimum and so its first derivative with respect to variable b should be zero.
dtdb=0
∴1c[bc−2bα(n−1)]=0
∴bD=2bα(n−1)
α=2(n−1)D.....(8)
⇒ Above equation gives required condition.
Here, value of α is independent of b. Hence for the case when b<<u, all paraxial rays, incident on the lens, will be focused at point O.
(ii) Now, for given gravitational lens,
W=K1log(K2b) (As per statement ) ....(9)
⇒ From equation (5) and (9).
t=1c[u+v=b2D+(n−1)K1log(K2b)]
∴t=1c[u+v+b22D+(n−1)K1{logK2−logb}]
∴dtdb=1c[0+0+12D(2b)+(n−1)K1{0−1b}]
∴dtdb=1c[bd−(n−1)K1b]........10
⇒ Now, according to Farmat.s principle we
have dtdb=0
bD=(n−1)K1b
∴b=(n−1)K1D
∴b=√(n−1)K1D.......(11)
⇒ Thus, those light rays which are incident on the lens at above height from S, contribute in the formation of image. Such image is having shape of a circular ring . If its angular radius is β then ,
Bη=arcradius
∴β==bb
=√(n−1)K1Db
=√(n−1)K1v2×uvu+v)
(∴ From equation (4) D =uvu+v)
∴β=√(n−)Kuv(u+v) .......(12)
⇒ Above equation gives required result.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - KUMAR PRAKASHANCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - SECTION-D (MULTIPLE CHOICE QUESTIONS (MCQs))(MCQs FROM .DARPAN. BASED ON TEXTBOOK)
26 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - KUMAR PRAKASHANCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - SECTION-D (MULTIPLE CHOICE QUESTIONS (MCQs))(MCQs FROM .DARPAN. BASED ON TEXTBOOK)(REFRACTION)
32 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - KUMAR PRAKASHANCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - SECTION-C (NCERT EXEMPLAR SOLUTION) (SHORT ANSWER TYPE QUESITONS)
6 Videos
- MOVING CHARGES AND MAGNETISMBOOK - KUMAR PRAKASHANCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - SECTION D (MCQs ASKED IN COMPETITIVE EXAMS)
34 Videos
- SAMPLE QUESTION PAPER BOOK - KUMAR PRAKASHANCHAPTER - SAMPLE QUESTION PAPER EXERCISE - PART-B SECTION-C
5 Videos
Similar Questions
Diameter of spherical mirror is 10 cm, what will be aperture of mirror ?
View SolutionRefraction index of medium-2 with respect to medium-1 is ...... .
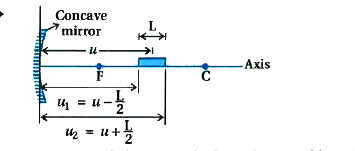
View SolutionA short object of length L is placed along the principal axis of a concave mirror away from focus. The object distance is u. If the mirror has a focal length f, what will be the length of the image ? You may take L<<|v−f|.
View SolutionElectric charge Q having mass M moves on a circular path of radius R with velocity →v, perpendicular to uniform magnetic field B. When a particle completes one revolution, work done by the field is _______
View SolutionTwo charges –q and +q are located at points (0, 0, –a) and (0, 0, a), respectively.
(a) What is the electrostatic potential at the points (0, 0, z) and (x, y, 0) ?
(b) Obtain the dependence of potential on the distance r of a point from the origin when r/a>>1 .
(c) How much work is done in moving a small test charge from the point (5,0,0) to (–7,0,0) along the x-axis? Does the answer change if the path of the test charge between the same points is not along the x-axis?
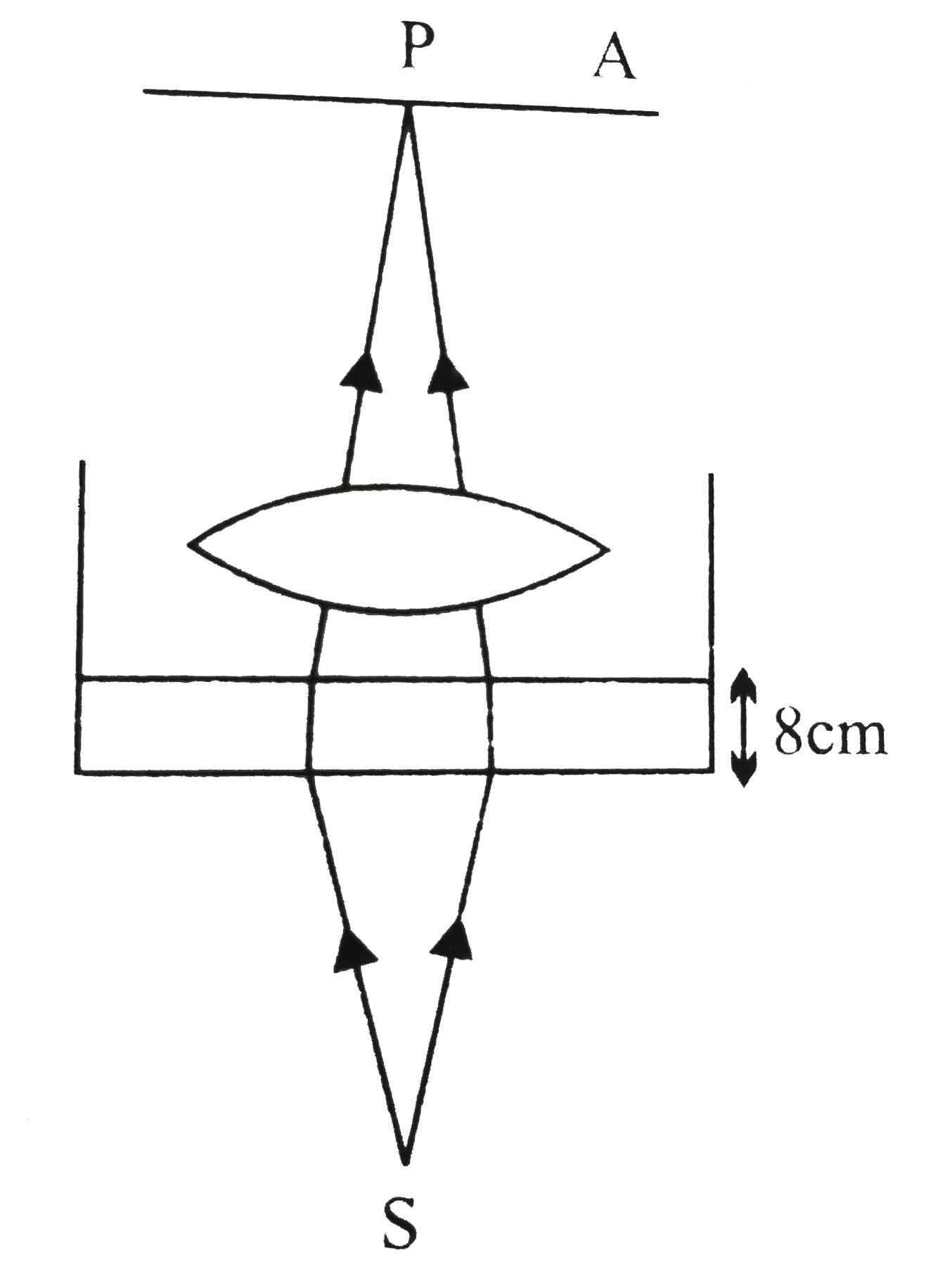
View SolutionA thin convex lens of refractive index μ=1.5 is placed between a point source of Light S and a screen A, shown in figure,. Light rays from the source S are brought to focus on the screen A, forming a point image P. The distance SP is equal to 50cm. Water (μ=4/3) is now poured into a vessel interposed between the object and the lens, and it is observed that when the water level is 8cm the screen has to be moved up by a distance of 6cm in order to get a sharp image. Find the focal length of the lens.
View SolutionA diverging lens of focal length 10cm is placed 10cm away in front of a plane mirror as shwon in figure. Light from a very far away source falls on the lens. An observer is situated some where in between lens and mirror, and observer is looking towards mirror. The observer will see the image behind teh mirror at a distance.
View SolutionIn the arrangement shown in figure, O is the object. An observer is to the left of convex lens and looking towards lens. The observer will see an image
View Solution(i) Consider a thin lens placed between a source (S) and an observer (O), Fig. Let the thickness of the lens vary as w (b) = w_0 - (b^2)/(prop) , where b is the vertical distance from the pole. w_0 is a constant. Using Fermat's principle, i.e., the time of transit for a ray between the source and observer is an exptremum, find the condition that al paraxial rays starting from the source will converge at a point O on the axis. Find the focal length. (ii) A gravitational lens may be assumed to have a varying width of the form w(b) = k_1 In ((k_2)/(b)) b_min lt b lt b_(max) w(b) = k_1 In ((k_2)/(b_(min))) b lt b_(min) Show that an observer will see an image of a point object as a ring about the center of the lens with an angular radius beta = sqrt(((n - 1) k_1 (u)/(v))/(u + v)) . .
View Solutionप्रकाश के दो बिंदु-स्रोतों के बीच की दूरी 30 सेमी है | एक स्त्रोत से 20 सेमी दूर एक उत्तल लेन्स रखने पर दोनों स्त्रोतों के प्रतिबिम्ब एक ही बिंदु पर बनते है | उस उत्तल लेन्स की फोकस-दूरी ज्ञात कीजिए |
View Solution(A) प्रकाश के दो बिन्दु स्त्रोतो के बीच की दूरी 30 सेमी है। एक स्त्रोत से 20 सेमी दूर एक उत्तल लेन्स रखने पर दोनों स्त्रोतो के प्रतिबिम्ब एक ही बिन्दु पर बनते हैं इस उत्तल लेन्स की फ़ोकस दूरी ज्ञात कीजिए। (B) लेन्स से प्रतिबिम्ब की दूरी क्या हैं ?
View SolutionIf the distance between the observer and source decresase with time, then it show that
View SolutionWhat is meant by Doppler effect? Discuss the following cases. (1) Sources in motion and Observer at rest (a) Source moves towards observer (a) Source moves towards observer (b) Source moves away from the observer (2) Observer in motion and Source at rest. (a) Observer moves towards Source. (b) Observer recedes away from the Source. (3) Both are in motion (a) Source and observer approach each other (b) Source and Observer resides from each other ( c) Source chases Observer (d) Observer chases Source.
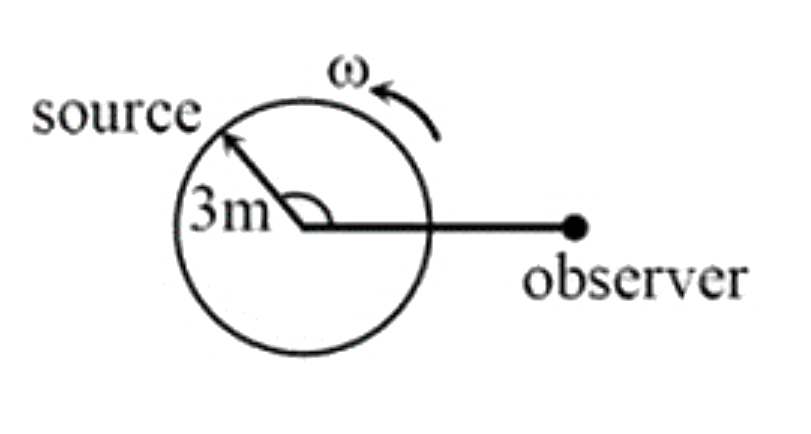
View SolutionA source is moving on a circle of radius 3m with constant angular velocity ω=5rads−1. If the observer is at a distance 5 cm from the centre of the circle, the time interval between the maximum and minimum frequency received by the observer is
View SolutionA sound source S is moving along a straight track with speed v, and is emitting sound of frequency v_0 (see figure). An observer is standing at a finite distance at the point O, from the track . The time variation of frequency heard by the observer is best respresent by : ( t_0 represents the instant when the distance between the source and observer is minimum )
View Solution
