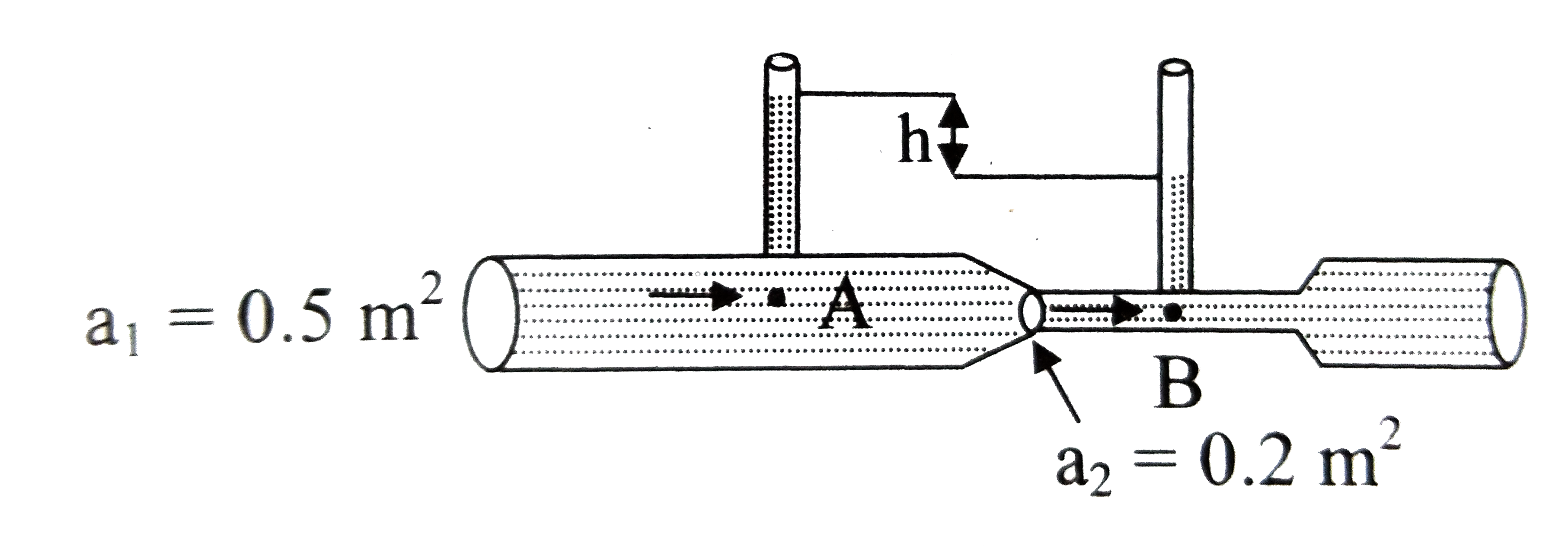
A liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross - section $A_{1} and A_{2}$ are $υ_{1} and υ_{2}$ respectively. The difference in the levels of the liquid in the two vertical tubes is h.

a) The volume of the liquid flowing through the tube in unit time is $A_{1} υ_{1}$ .
b) $υ_{2} - υ_{1} = \sqrt{2 g h}$ c) $υ_{2}^{2} - υ_{1}^{2} = 2 g h$
d) The energy per unit mass of the liquid is the same in both sections of the tube.

A

a, c and d are correct

B

c and d are correct

C

a, b and d are correct

D

All are correct

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

|

Class 11 PHYSICS PROPERTIES OF SOLIDS AND FLUIDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

A liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross section $A_{1}$ and $A_{2}$ are $v_{1}$ and $v_{2}$ respectively. The difference in the levels of the liquid in the two vertical tubes is $h$ . Then

Athe volume of the liquid flowing through the tube in unit time is $A_{1} v_{1}$
B $v_{2} - v_{1} = \sqrt{2 g h}$
C $v_{2}^{2} - v_{1}^{2} = 2 g h$
Dthe energy per unit mass of the liquid is the same in both sections of the tube
A liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section $A_{1}$ and $A_{2}$ and $v_{1}$ and $v_{2}$ respectively. The difference in the levels of the liquid in the two vertical tubes is $h$ , then

A $v_{2}^{2} - v_{1}^{2} = 2 g h$
B $v_{2}^{2} + v_{1}^{2} = 2 g h$
C $v_{2}^{2} - v_{1}^{2} = g h$
D $v_{2}^{2} + v_{1}^{2} = g h$
A liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section $A_{1}$ and $A_{2}$ and $v_{1}$ and $v_{2}$ respectively. The differnece in the levels of the liquid in the two vertical tubes is $h$ . then

A $v_{2}^{2} - v_{1}^{2} = 2 g h$
B $v_{2}^{2} + v_{1}^{2} = 2 g h$
C $v_{2}^{2} - v_{1}^{2} = g h$
D $v_{2}^{2} + v_{1}^{2} = g h$

AAKASH SERIES-MECHANICAL PROPERTIES OF FLUIDS -EXERCISE-IA

Home
Ask Doubt
Profile