A glass tube of uniform internal radius (r ) has a valve separating the two identical ends. Initially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble of radius r. End 2 has sub-hemispherical sop bubble as shown in figure. Just after opening the valve,
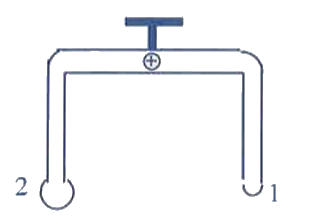
Air from end 1 flows towards end 2. No change in the volume of the soap bubbles
Air from end 1 flows towards end 2. Volume of the soap buble at end 1 decreases
No change occurs
Air form end 2 flows toward end 1. Volume of the soap bubble at end 1 increases
The correct Answer is:B
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDS BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-IB (ASSERTION & REASON)
46 Videos
- MECHANICAL PROPERTIES OF FLUIDS BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-2
68 Videos
- MECHANICAL PROPERTIES OF FLUIDS BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-3
43 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
108 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE - 3
26 Videos
Similar Questions
A glass tube of uniform internal radius(r) has a valve separating the two identical ends. Intially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble or radius r. End 2 has sub-hemispherical soap bubble as shown in figure. Just after opening the valve,

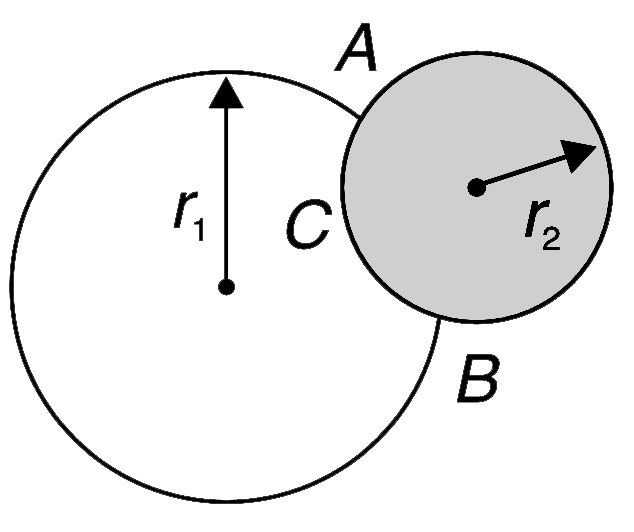
View SolutionTwo soap bubbles of radii r1andr2 are attached as shown. Find the radius of curvature of the common film ACB.
View Solution
Knowledge Check
A glass tube of uniform internal radius(r) has a valve separating the two identical ends. Intially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble or radius r. End 2 has sub-hemispherical soap bubble as shown in figure. Just after opening the valve,
 A(a) air from end 1 flows towards end 2. No change in the volume of the soap bubblesB(b) air from end 1 flows towards end 2. Volume of the soap bubble at end 1 decreasesC(c) no changes occursD(d) air from end 2 flows towards end 1. volume of the soap bubble at end 1 increases
A(a) air from end 1 flows towards end 2. No change in the volume of the soap bubblesB(b) air from end 1 flows towards end 2. Volume of the soap bubble at end 1 decreasesC(c) no changes occursD(d) air from end 2 flows towards end 1. volume of the soap bubble at end 1 increasesTwo spherical soap bubbles of radii r1 and r2 in vacuume collapse under isothermal condition. The resulting bubble has radius R such that
AR=r1+r2BR=(r1+r2)12CR=√r21+r22DR=[(r2r2(r1+r2)]Two spherical soap bubbles of radii r1andr2 in vaccum coalesce under isothermal conditions. The resulting bubble has a radius R such that
A(r1+r2)/2BR=[r1r2]/r1+r+(2)CR=√(r21+r22)DR=r1+r2
Two soap bubbles of radius r1 and r2 combine. Find radius of curvature of the common surface separating them.

View SolutionTwo soap bubbles with radius 2r and 3r come in contact. Their common surface has a radius of curvature nr, then find the value of n
View SolutionA semicircular metallic disc of radius R has two small cavities of radii r1and r2 as shown in the figure. On heating the disc

View SolutionTwo spherical soap bubbles of a radii 1 cm and 2 cm vacuum coalesce under isothermal conditions . The resultant bubble has a radius of
View SolutionTwo unequal soap bubbles are formed one on each side of a tube closed in the middle by a tap. What happens when the tap is opened to put the two bubbles in communication?
View Solution
