In the following figures, PQ = LM, Q is the midpoint of PR and M is the midpoint of LN. Using the axioms, prove that PR = LN.

Step by step video & image solution for In the following figures, PQ = LM, Q is the midpoint of PR and M is the midpoint of LN. Using the axioms, prove that PR = LN. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- INTRODUCTION TO EUCLID.S GEOMETRYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - INTRODUCTION TO EUCLID.S GEOMETRYEXERCISE - MULTIPLE CHOICE QUESTIONS
3 Videos
- INTRODUCTION TO EUCLID.S GEOMETRYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - INTRODUCTION TO EUCLID.S GEOMETRYEXERCISE - EXERCISE 5.2
2 Videos
- CIRCLES BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLES EXERCISE - SUM TO ENRICH REMAMBER
6 Videos
- LINE AND ANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINE AND ANGLESEXERCISE - Multiple Choice Questions MCQs)
10 Videos
Similar Questions
Knowledge Check
If S is the midpoint of a straight line PQ and R is a point different from S , such that PR = RQ , then
A∠PRS=90∘B∠QRS=90∘C∠PSR=90∘D∠QSR<90∘In the following figure, Q is a point on PR and S is a point on TR. QS is drawn and ∠RPT=∠RQS.
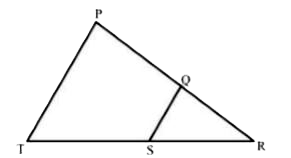
Which of these criteria can be used to prove that ΔRSQ is similar to ΔRTP?AAAA similarity criterion BBSAS similarity criterionCSSS similarity criterionDRHS similarity criterionIn the given figure, ABCD is a square. M is the midpoint of AB and PQ⊥CM. Which of the following statements is not true ?
 AAM = MBBCP = CQCCP = CBDPM = MQ
AAM = MBBCP = CQCCP = CBDPM = MQ
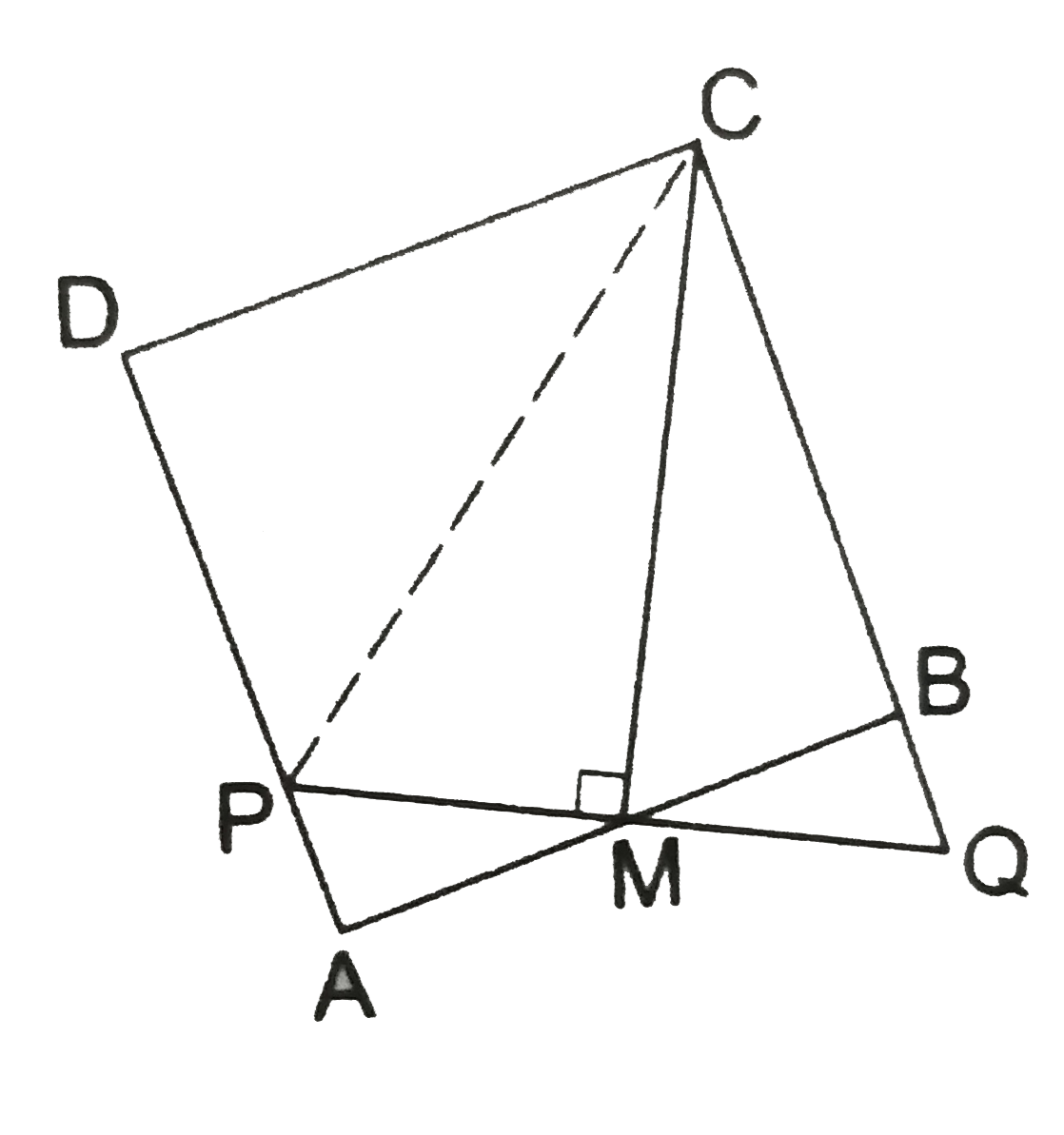
In the given figure, ABCD is a square, M is the midpoint of AB and PQ⊥CM meets AD at P and CB produced at Q. Prove that (i) PA = QB and (ii) CP=AB+PA.
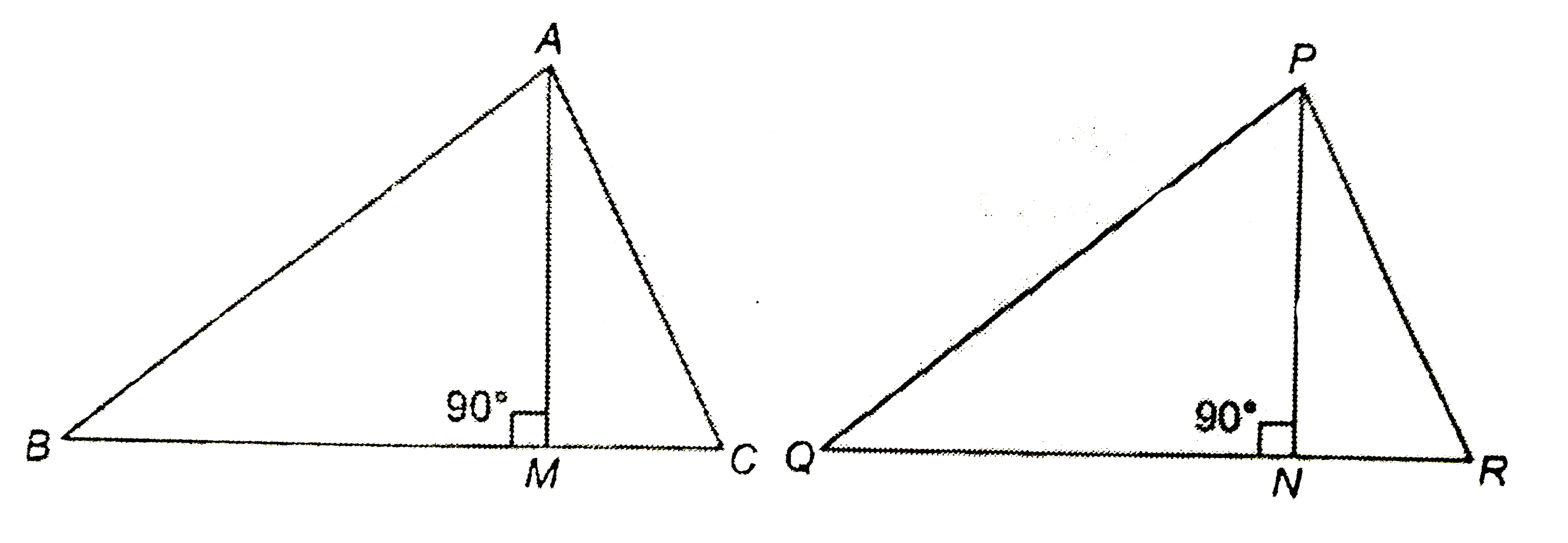
View SolutionIn the following figures, AB=PQ,AC=PR and AM=PN. Prove that ΔABC≅ΔPQR.
View SolutionIn the adjoining figure, PQ=PR. Show that PS>PQ.
View SolutionIn the given figure, points S,T and U are the midpoints of sides PQ,QR and PR respectively. IF PV⊥QR, then prove that □ SVTU is a cyclic quadrilateral.
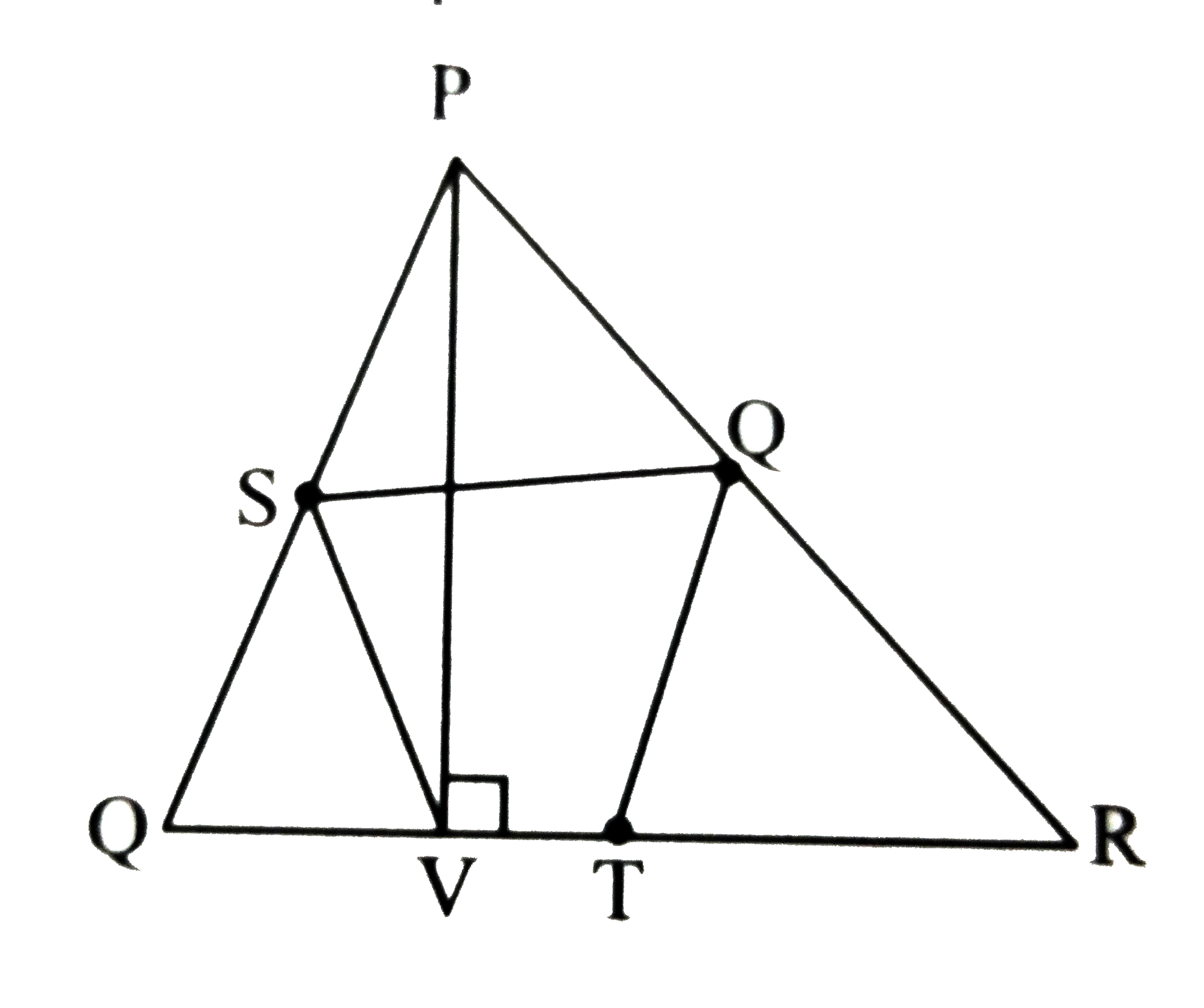
View Solution
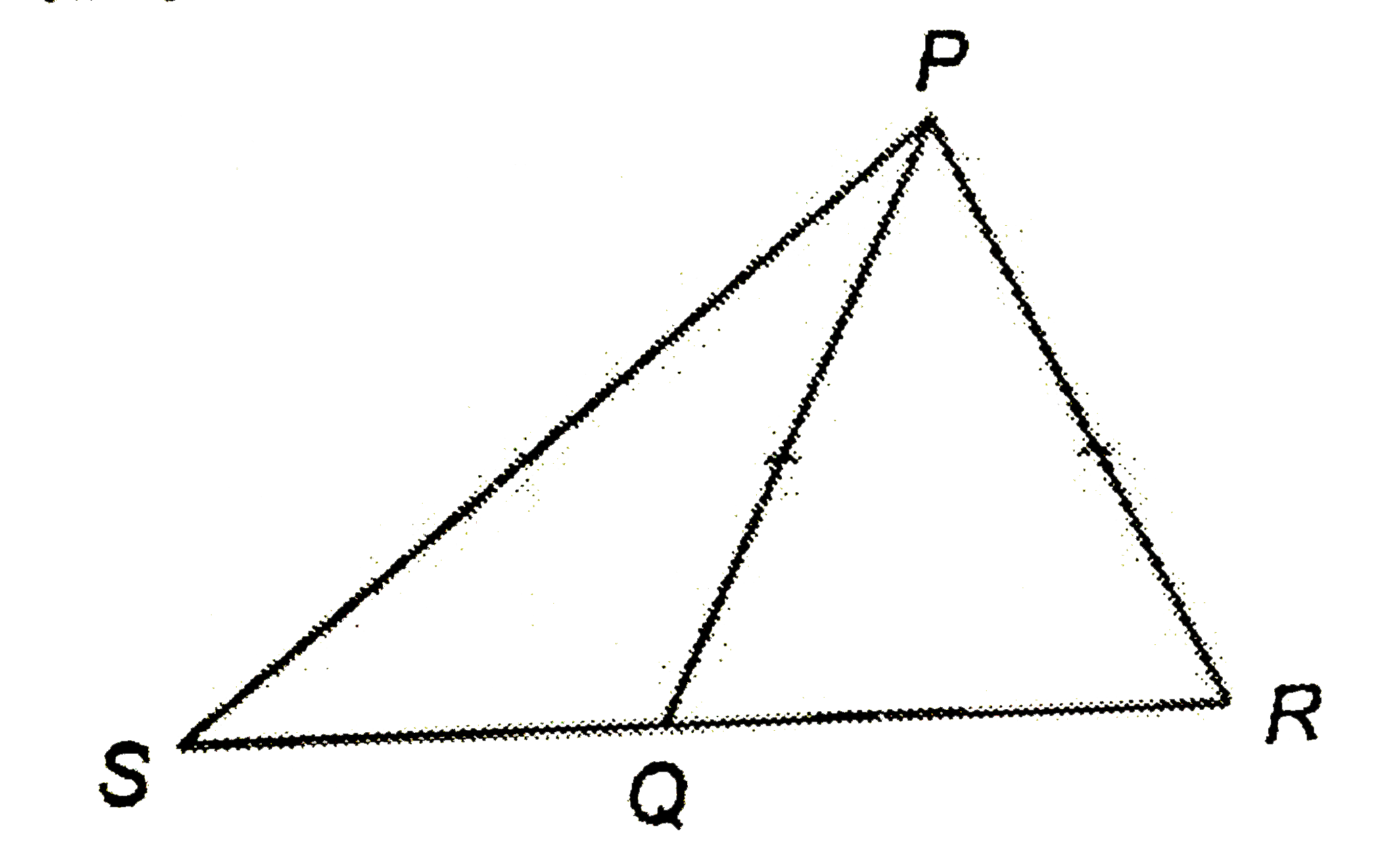
In the figure , S is the midpoint of seg PQ . Line ST || side QR and PT =5 cm , then find PR. Justify your answer.
View Solution
