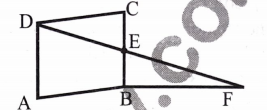
In the given figure, ABCD is a square, M is the midpoint of AB and PQ⊥CM meets AD at P and CB produced at Q. Prove that (i) PA = QB and (ii) CP=AB+PA.
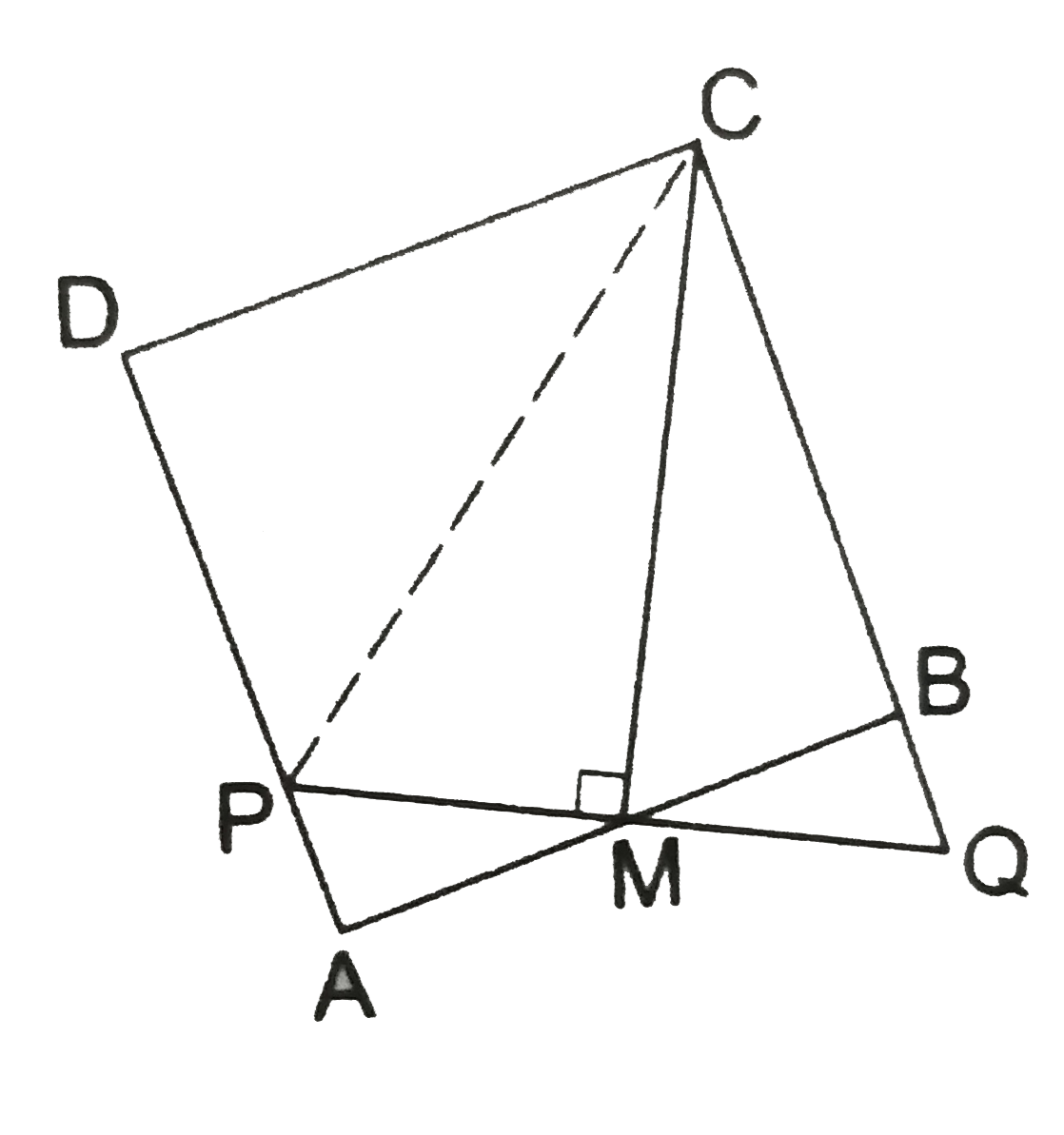
GIVEN A square ABCD in which M is the midpoint of AB.PQ⊥CM meets AD at P and CB produced at Q.
TO PROVE (i) PA=QBand(ii)CP=AB+PA.
PROOF (i) In ΔPAMandΔQBM, we have
AM=BM (∵ M is the midpoint of AB)
∠PAM=∠QBM (each equal to 90∘)
∠AMP=∠BMQ (vertically opp. ∠s)
∴ ΔPAM≅ΔQBM (AAS-criteria).
Hence, PA=QB (c.p.c.t.).
(ii) Join PC.
Now, in ΔCMPandΔCMQ, we have
PM=QM (∵ΔPAM≅DetlaQBM)
∠CMP=∠CMQ (each equal to 90∘)
CM=CM (common)
∴ ΔCMP≅ΔCMQ (SAS-criteria).
∴ CP=CQ (c.p.c.t.).
⇒ CP=CB+CQ=AB+PA [∵CB=ABandQB=PA].
Hence, CP=AB+PA.
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A
27 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
Knowledge Check
In the given figure, ABCD is a square. M is the midpoint of AB and PQ⊥CM. Which of the following statements is not true ?
 AAM = MBBCP = CQCCP = CBDPM = MQ
AAM = MBBCP = CQCCP = CBDPM = MQ
In the given figure, ABCD is a parallelogram and E is the midpoint of side BC. If DE and AB when produced meet at F, prove that AF = 2AB.

View SolutionIn the given figure, ABCD is a quadrilateral in which AB∣∣DC and P is the midpoint of BC. On producing, AP and DC meet at Q. Prove that (i) AB=CQ, (ii) DQ=DC+AB
View SolutionIn the given figure ABCD is a quadrilateral in which AB||DC and P is the midpoint of BC. On producing, AP and DC meet at Q. Prove that (i)AB=CQ,(ii)DQ=DC+AB.

View SolutionIn the given figure L and M are the midpoints of AB and BC respectivcely
(i) If AB= BC prove that AL = MC
(ii) If BL = BM prove that AB=BC
View SolutionP is the mid-point of side AB of parallelogram ABCD. A line drawn from B parallel to PD meets CD at Q and AD produce at R. Prove that :
(i) AR = 2BC (ii) BR= 2BQ
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A Line through B parallel to PD meets DC at Q and AD produced at R . Prove that (i) AR=2BC (ii) BR=2BQ.
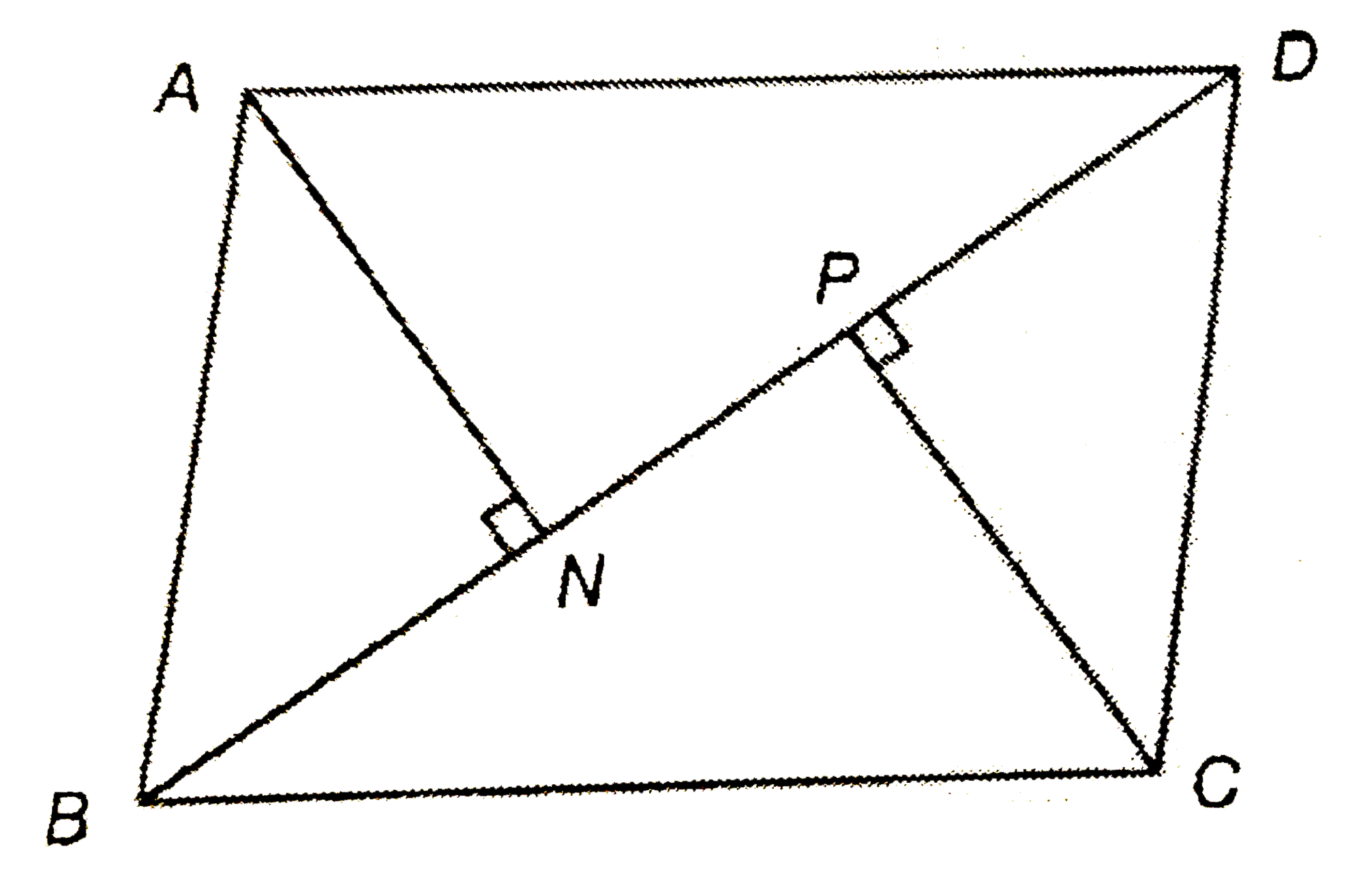
View SolutionIn the given figure, ABCD is a parallelogram in which AN and CP are perpendiculars on diagonal BD. Prove that :
(i) ΔADN=ΔCBP
(ii)AN=CP
View Solution