In parallelogram ABCD, diagonals AC and BD are equal. Find the measure of ∠ ABC and prove that the quadrilateral ABCD is a rectangle.
To solve the problem, we need to find the measure of angle ABC in parallelogram ABCD where the diagonals AC and BD are equal, and then prove that ABCD is a rectangle.
1. Identify the Properties of the Parallelogram:
- In parallelogram ABCD, opposite sides are equal (AB = CD and AD = BC).
- The diagonals bisect each other.
2. Given Information:
- Diagonals AC and BD are equal (AC = BD).
3. Congruent Triangles:
- Consider triangles ADB and CDB.
- We have:
- AC = BD (given)
- AD = BC (opposite sides of parallelogram)
- AB = CD (opposite sides of parallelogram)
- By the Side-Angle-Side (SAS) congruence criterion, triangles ADB and CDB are congruent.
4. Conclusion from Congruent Triangles:
- Since triangles ADB and CDB are congruent, we have:
- Angle ADB = Angle CDB (corresponding angles in congruent triangles)
- Let angle ABC = x. Then angle ADB = x as well.
5. Using Parallel Lines:
- Since AD is parallel to BC, we can apply the property of alternate interior angles:
- Angle ABC + Angle DAB = 180° (angles on the same side of the transversal).
- Since angle DAB is also equal to x (from the congruence of triangles), we can write:
- x + x = 180°
- 2x = 180°
- x = 90°.
6. Measure of Angle ABC:
- Therefore, angle ABC = 90°.
7. Proving ABCD is a Rectangle:
- In a parallelogram, if one angle is 90°, then all angles are 90°.
- Since angle ABC = 90°, angle DAB = 90° (as shown earlier).
- By the property of parallelograms, opposite angles are equal:
- Therefore, angle ADC = 90° and angle BCD = 90°.
- Since all angles in parallelogram ABCD are 90°, we conclude that ABCD is a rectangle.
Final Conclusion:
- The measure of angle ABC is 90°, and quadrilateral ABCD is a rectangle.
- In parallelogram ABCD, opposite sides are equal (AB = CD and AD = BC).
- The diagonals bisect each other.
- Diagonals AC and BD are equal (AC = BD).
- Consider triangles ADB and CDB.
- We have:
- AC = BD (given)
- AD = BC (opposite sides of parallelogram)
- AB = CD (opposite sides of parallelogram)
- By the Side-Angle-Side (SAS) congruence criterion, triangles ADB and CDB are congruent.
- Since triangles ADB and CDB are congruent, we have:
- Angle ADB = Angle CDB (corresponding angles in congruent triangles)
- Let angle ABC = x. Then angle ADB = x as well.
- Since AD is parallel to BC, we can apply the property of alternate interior angles:
- Angle ABC + Angle DAB = 180° (angles on the same side of the transversal).
- Since angle DAB is also equal to x (from the congruence of triangles), we can write:
- x + x = 180°
- 2x = 180°
- x = 90°.
- Therefore, angle ABC = 90°.
- In a parallelogram, if one angle is 90°, then all angles are 90°.
- Since angle ABC = 90°, angle DAB = 90° (as shown earlier).
- By the property of parallelograms, opposite angles are equal:
- Therefore, angle ADC = 90° and angle BCD = 90°.
- Since all angles in parallelogram ABCD are 90°, we conclude that ABCD is a rectangle.
- The measure of angle ABC is 90°, and quadrilateral ABCD is a rectangle.
Topper's Solved these Questions
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - MULTIPLE CHOICE QUESTIONS
15 Videos
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - SUMS TO ENRICH REMEMBER
9 Videos
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.5
4 Videos
- SURFACE AREAS AND VOLUMESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - MULTIPLE CHOICE QUESTIONS
18 Videos
Similar Questions
ABCD is a parallelogram, if the two diagonals are equal, find the measure of ∠ABC.
View SolutionIn a parallelogram ABCD diagonals AC and BD intersect at O and AC=6.8cm and BD=13.6cm. Find the measures of OC and OD.
View SolutionIn a parallelogram ABCD diagonals AC and BD intersect at O and AC =12.6 cm and BD = 9.4 cm. Find the measures of OC and OD.
View SolutionIf the diagonals AC, BD of a quadrilateral ABCD, intersect at O, and separate the quadrilateral into four triangles of equal area, show that quadrilateral ABCD is a parallelogram.
View SolutionGiven Parallelogram ABCD in which diagonals AC and BD at M.Prove M is mid-point of LN.
View SolutionFind the measure of angle ABC (in degrees) in the parallelogram ABCD as shown in the given figure:
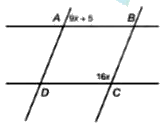
View SolutionACandBD are chords of a circle that bisect each other. Prove that:AC and BD are diameter. ABCD is a rectangle
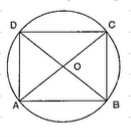
View SolutionIn a parallelogram ABCD diagonals AC and BD intersect at O and AC = 7.4 cm and BD = 6.2 cm. Find the length of AO and BO.
View SolutionIn Quadrilateral ABCD, diagonal AC & BD intersect at "O". By Diagonals area of quadrilateral ABCD is divided into 4 parts. Find area of the fourth part (x), area of other 3 parts is mentioned in the figure.
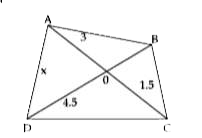
View SolutionBD intersect at 0 and AC = 12.8 cm and BD-7.6 In a parallelogram ABCD, diagonals AC and cm. Find the measures of OC and OD
View Solution
