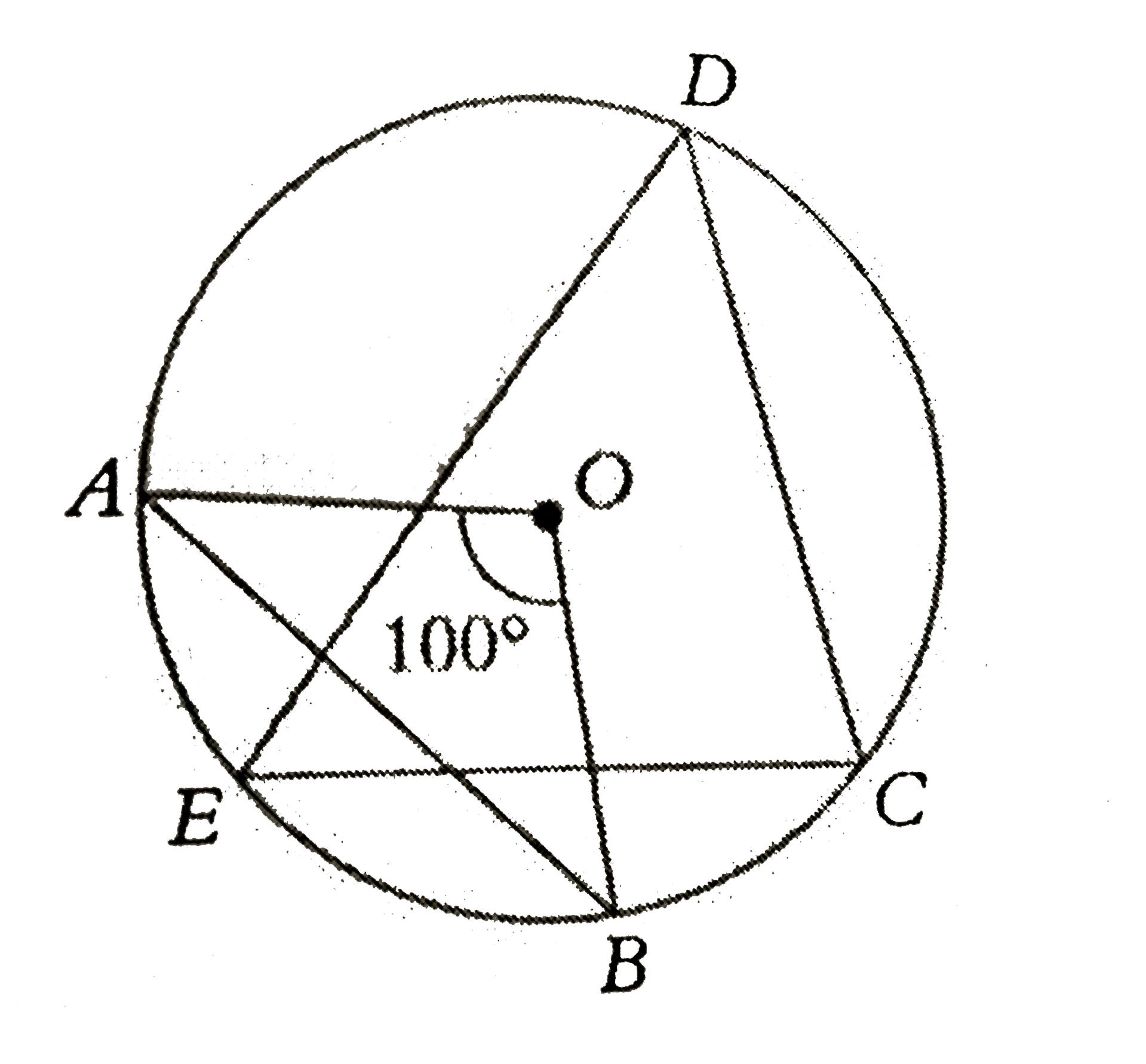In a circle with centre P.AB and CD are congruent chords. If ∠PAB=40∘, then ∠CPD=
40∘
80∘
100∘
50∘
The correct Answer is:C
To solve the problem, we need to find the measure of angle ∠CPD given that ∠PAB=40∘ and that chords AB and CD are congruent.
1. Identify the Given Information:
- We have a circle with center P.
- Chords AB and CD are congruent.
- ∠PAB=40∘.
2. Recognize Properties of the Circle:
- Since AB and CD are congruent chords, the distances from the center P to the chords are equal.
- The triangle APB is isosceles because PA=PB (both are radii of the circle).
3. Determine Angles in Triangle APB:
- In triangle APB, since PA=PB, we have ∠PAB=∠PBA=40∘.
- The sum of angles in a triangle is 180∘. Therefore:
∠APB+∠PAB+∠PBA=180∘
∠APB+40∘+40∘=180∘
∠APB+80∘=180∘
∠APB=180∘−80∘=100∘
4. Use the Property of Vertically Opposite Angles:
- The angle ∠CPD is vertically opposite to ∠APB.
- Therefore, we have:
∠CPD=∠APB=100∘
5. Conclusion:
- The measure of angle ∠CPD is 100∘.
Final Answer:
∠CPD=100∘
- We have a circle with center P.
- Chords AB and CD are congruent.
- ∠PAB=40∘.
- Since AB and CD are congruent chords, the distances from the center P to the chords are equal.
- The triangle APB is isosceles because PA=PB (both are radii of the circle).
- In triangle APB, since PA=PB, we have ∠PAB=∠PBA=40∘.
- The sum of angles in a triangle is 180∘. Therefore:
∠APB+∠PAB+∠PBA=180∘
∠APB+40∘+40∘=180∘
∠APB+80∘=180∘
∠APB=180∘−80∘=100∘
- The angle ∠CPD is vertically opposite to ∠APB.
- Therefore, we have:
∠CPD=∠APB=100∘
- The measure of angle ∠CPD is 100∘.
∠CPD=100∘
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLES EXERCISE - SUM TO ENRICH REMAMBER6videos
CIRCLES
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLES EXERCISE - SKILL TESTING EXERCISE11videos
CIRCLES
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - INTRODUCTION TO EUCLID.S GEOMETRYEXERCISE - MULTIPLE CHOICE QUESTIONS3videos
INTRODUCTION TO EUCLID.S GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
AB is a diameter of the circle with centre O, CD is chord of the circle. If ∠BOC=120∘, then the value of ∠ADC is
A42∘B30∘C60∘D35∘ - Question 2 - Select One
Two chords AB, CD of a circle with centre O intersect each other at P. ∠ADP=23∘ and ∠APC=70∘, then the ∠BCDis
A45∘B47∘C57∘D67∘ - Question 3 - Select One
Two chords AB and CD of a circle with centre o intersect each other at the point P. If ∠AOD=20∘ and ∠BOC=30∘, then ∠BPCis equal to:
A50∘B20∘C25∘D30∘
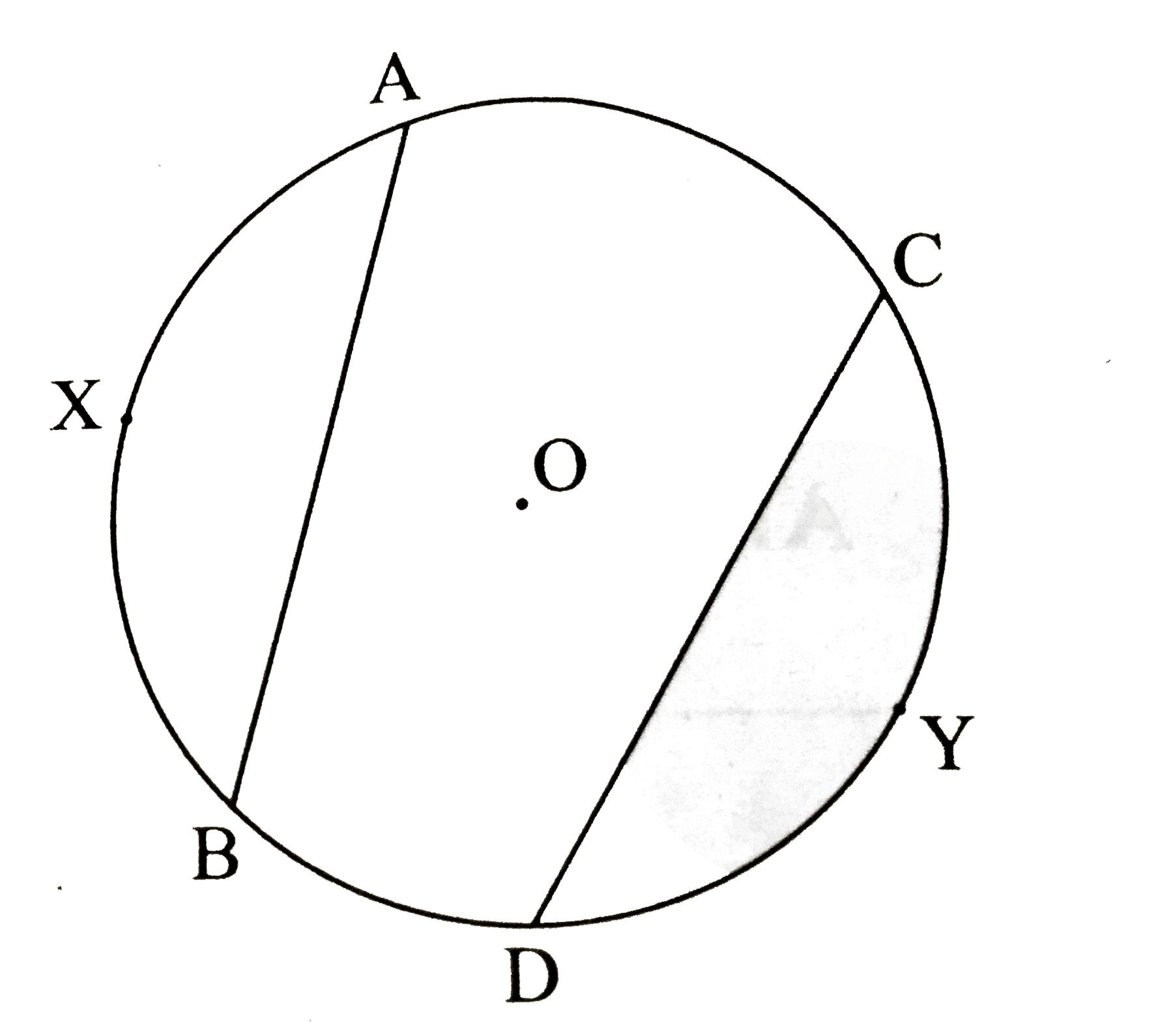
Chords AB andCD of a circle with centre O are congruent. If m(arc AXB) =120∘ then what is the m(arc( CYD).
 View Solution
View SolutionAB and CD are two chords of circle with centre O and are perpendicular to each other. If ∠OAC=25∘ then ∠BCD = ?
View SolutionIn the following figure, O is the centre of the circle. AB and CD are equal chords. If ∠AOB=100∘ , Find the ∠CED.
 View Solution
View SolutionIn a circle with centre O. AB and CD are parallel chords lying on opposite sides of a diameter parallel to them. If AB = 30 cm, CD - 48 cm and the distance between AB and CD is 27 cm, find the radius of the circle.
View SolutionTwo chords AB and CD of a circle with centre O, intersect each other at P. If ∠AOD=100∘and∠BOC=70∘, then the value of ∠APC is
View Solution