In a circle with centre P, AB is a minor arc. Point Ris a point other than A and B on major arc AB. If ∠ARB=80∘, then ∠APB=........
40∘
80∘
160∘
60∘
The correct Answer is:C
To solve the problem, we need to find the angle ∠APB given that ∠ARB=80∘.
1. Understanding the Angles:
- We have a circle with center P.
- AB is a minor arc, and R is a point on the major arc AB.
- The angle ∠ARB is given as 80∘.
2. Using the Angle Subtended by an Arc:
- According to the properties of circles, the angle subtended at the center of the circle by an arc is twice the angle subtended at any point on the circumference of the circle.
- This means that ∠APB (the angle at the center) is related to ∠ARB (the angle at the circumference).
3. Applying the Relationship:
- We can express this relationship mathematically as:
∠APB=2×∠ARB
4. Substituting the Known Value:
- We know that ∠ARB=80∘.
- Therefore, we substitute this value into the equation:
∠APB=2×80∘=160∘
5. Final Answer:
- Thus, the value of ∠APB is 160∘.
Summary of the Solution:
∠APB=160∘
- We have a circle with center P.
- AB is a minor arc, and R is a point on the major arc AB.
- The angle ∠ARB is given as 80∘.
- According to the properties of circles, the angle subtended at the center of the circle by an arc is twice the angle subtended at any point on the circumference of the circle.
- This means that ∠APB (the angle at the center) is related to ∠ARB (the angle at the circumference).
- We can express this relationship mathematically as:
∠APB=2×∠ARB
- We know that ∠ARB=80∘.
- Therefore, we substitute this value into the equation:
∠APB=2×80∘=160∘
- Thus, the value of ∠APB is 160∘.
∠APB=160∘
Topper's Solved these Questions
- CIRCLES BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLES EXERCISE - SUM TO ENRICH REMAMBER
6 Videos
- CIRCLES BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLES EXERCISE - SKILL TESTING EXERCISE
11 Videos
- INTRODUCTION TO EUCLID.S GEOMETRYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - INTRODUCTION TO EUCLID.S GEOMETRYEXERCISE - MULTIPLE CHOICE QUESTIONS
3 Videos
Similar Questions
In the following figure, AB is an arc of the circle, C and D are the points on the circle. If ∠ACB=30∘, Find ∠ADB.

View SolutionIn a circle with centre O, suppose A, P, B are three points on its circumference such that P is the mid-point of minor arc AB. Suppose ∠AOB=θ Area(△AOB)Area(△APB)=√5+2 If ∠AOB is doubled to 2θ, then the ratio area(△AOB)area(△APB) is
View Solution
Knowledge Check
In a circle with centre P, AB is a minor arc. Point Ris a point other than A and B on major arc ifANGLE∠APB=150∘. then ∠ARB=.........
A150∘B75∘C50∘D100∘A circle with centre O is given and C is a point on its minor arc AB. If ∠AOB=100∘ then ∠ACB is equal to which of the following?
AA)80∘BB)90∘CC)100∘DD)130∘C is a point on the minor arc AB a circle with centre O. If ∠AOB=100∘, what is ∠ACB ?
A80∘B90∘C100∘D130∘
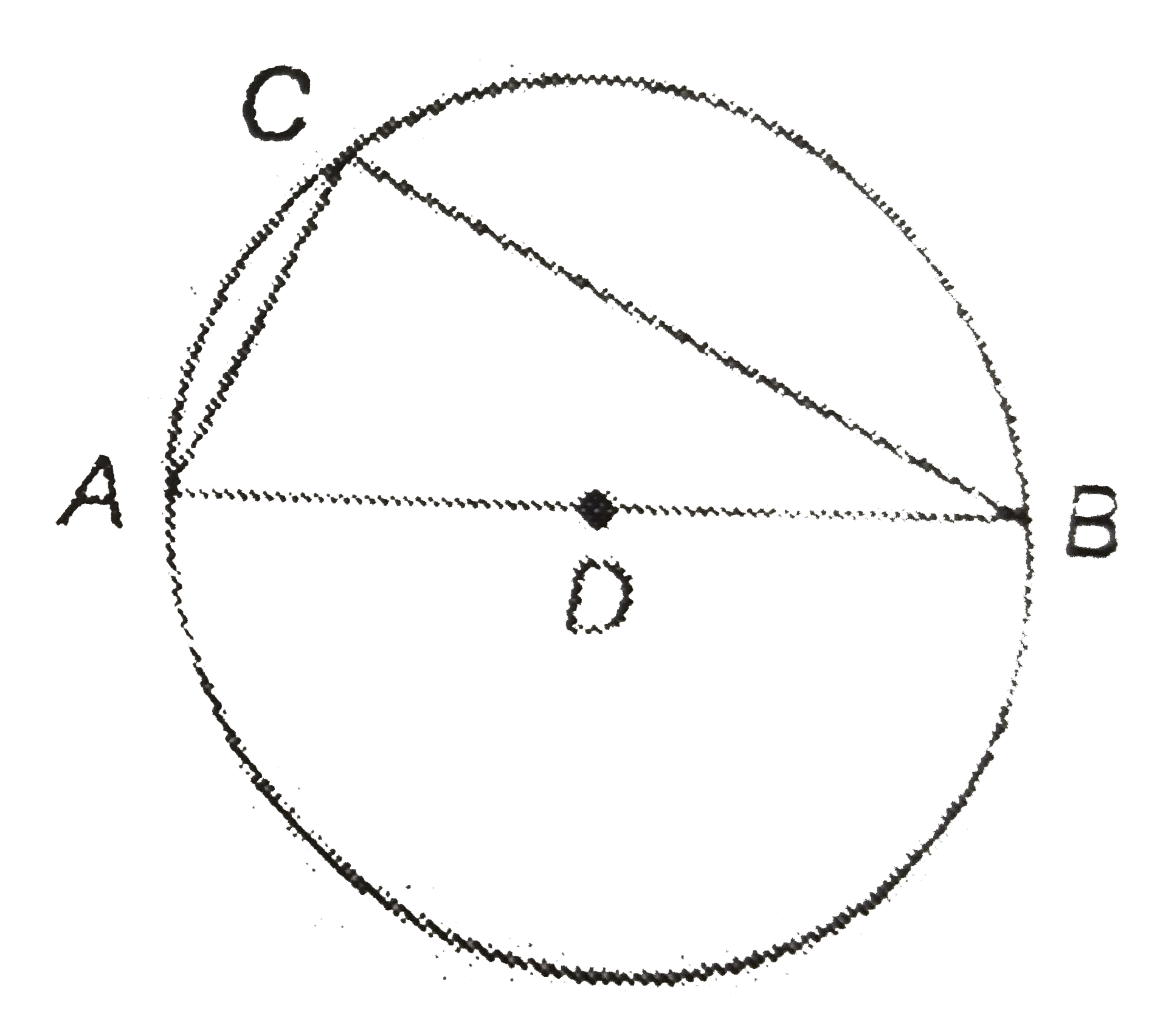
Show that any angle in a semi-circle is a right angle.
The following arc the steps involved in showing the above result. Arrange them in sequential order.
A) ∴∠ACB=180∘2=90∘
B) The angle subtended by an arc at the center is double of the angle subtended by the same arc at any point on the remaining part of the circle.
c) Let AB be a diameter of a circle with center D and C be any point on the circle. Join AC and BC.
D) ∴∠AD=2×∠ACB
180∘=2∠ACB(∴∠ADB=180∘)
View SolutionP is a point on a circle with centre 0. If P is equidistant from the two radii OA and OB, prove that arc AP=arcBP.
View SolutionAB is the diameter of a circle with centre O. The tangent at a point C on the circle meets AB produced at Q. If ∠CAB=42∘, then what is the measure of ∠CQA?
AB एक वृत्त का व्यास है जिसका केंद्र O है | वत्त पर स्थित एक बिंदु C से गुजरने वाली स्पर्श रेखा AB से Q पर मिलती है | यदि ∠CAB=42∘ है, तो ∠CQA का मान क्या होगा ?
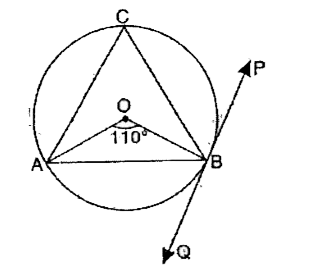
View SolutionIn the given figure, AB is a chord of the circle with centre O and PQ is a tangent at point B of the circle. If ∠AOB=110∘, then ∠ ABQ is
View SolutionAB is a diameter of a circle with centre O. CD is a chord equal to the radius of the circle. AC and BD are produced to meet at P. Then the measure of ∠APB is:
View Solution
