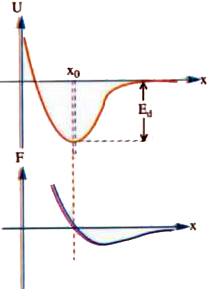
The potential energy of a diatomic molecule is given as $U = \frac{a}{x^{12}} - \frac{b}{x^{6}}$ . Find the (i) stable equilibrium distance of separation between two atoms, (ii) force on each atom as the function of separating distance x.

Text Solution

Verified by Experts

(i) Let us assume that the stable equilibrium separation between the atoms is $x_{0}$ , where the potential energy U is miniumum. To find $x_{0}$ , we take the derivative of U and equate it to zero ,
That means $\frac{d U}{d x} = 0$ where $U = \frac{a}{x^{12}} - \frac{b}{x^{6}}$
Then, we have $- \frac{12 a}{x_{0}^{13}} + \frac{6 b}{x_{0}^{7}} = 0$
This gives $x_{0} = {(\frac{2 a}{b})}^{1 / 6}$
(ii) The force between the atoms at any value of x is
$F = - \frac{d U}{d x} = - \frac{d}{d x} (\frac{a}{x^{12}} - \frac{b}{x^{6}}) = \frac{12 a}{x^{13}} - \frac{6 b}{x^{7}}$ .

|

Updated on:21/07/2023

Class 11 PHYSICS WORK, ENERGY AND POWER

Similar Questions

Knowledge Check

Question 1 - Select One
The potential energy between two atoms in a molecule is given by, $U_{(x)} = \frac{a}{x^{12}} - \frac{b}{x^{6}}$ , where a and b are positive constant and x is the distance between the atoms. The atoms is an stable equilibrium, when-
A ${(\frac{2 a}{b})}^{1 / 6}$
B ${(\frac{a}{b})}^{1 / 6}$
C ${(\frac{b}{2 a})}^{1 / 6}$
D ${(\frac{b}{a})}^{1 / 6}$
Question 2 - Select One
The potential energy function for a diatomic molecule is $U (x) = \frac{a}{x^{12}} - \frac{b}{x^{6}}$ entered In stable equilibrium, the distance between the particles is
A ${(\frac{2 a}{b})}^{1 / 6}$
B ${(\frac{a}{b})}^{1 / 6}$
C ${(\frac{b}{2 a})}^{1 / 6}$
D ${(\frac{b}{a})}^{1 / 6}$
Question 3 - Select One
The potential energy between two atoms in a molecule is given by $U (x) = \frac{1}{x^{12}} - {(b)}^{x^{6}}$ , where a and b are positive constants and x is the distance between the atoms. The atom is in stable equilibirum when
A $x = 6 \sqrt{\frac{11 a}{5 b}}$
B $x = 6 \sqrt{\frac{a}{2 b}}$
C $x = 0$
D $x = 6 \sqrt{\frac{2 a}{b}}$

Recommended Questions

Home
Ask Doubt
Profile