If the potential energy between two molecules is given by , then at equilibrium , separation between molecules , and the potential energy are :
To solve the problem, we need to find the equilibrium separation between two molecules and the potential energy at that separation given the potential energy function:
U=−Ar6+Br12
Step 1: Find the Force from the Potential Energy
The force F between the molecules can be derived from the potential energy U using the relation:
F=−dUdr
Step 2: Differentiate the Potential Energy
Now, we differentiate U:
U=−Ar6+Br12
Differentiating with respect to r:
dUdr=ddr(−Ar6)+ddr(Br12)
Using the power rule for differentiation:
dUdr=6Ar7−12Br13
Thus, the force F becomes:
F=−(6Ar7−12Br13)=−6Ar7+12Br13
Step 3: Set the Force to Zero for Equilibrium
At equilibrium, the force F is zero:
−6Ar7+12Br13=0
Rearranging gives:
12Br13=6Ar7
Step 4: Solve for r
Cross-multiplying gives:
12Br7=6Ar13
Dividing both sides by r7 (assuming r≠0):
12B=6Ar6
Thus:
r6=12B6A=2BA
Taking the sixth root gives us the equilibrium separation:
r=(2BA)16
Step 5: Calculate the Potential Energy at Equilibrium
Now, we substitute r back into the potential energy function to find U:
U=−Ar6+Br12
Substituting r6=2BA:
U=−A2BA+B(2BA)2
Calculating each term:
1. The first term:
−A22B
2. The second term:
B4B2A2=A24B
Combining these gives:
U=−A22B+A24B=−2A24B+A24B=−A24B
Final Results
Thus, at equilibrium, the separation between the molecules is:
r=(2BA)16
And the potential energy at this separation is:
U=−A24B
Topper's Solved these Questions
Similar Questions
Distinguish between Kinetic energy and potential energy
View SolutionPotential energy in a field is given by U=−Ar6+Br11 then find the value of r for equilibrium position.
View SolutionDifferentiate between Kinetic energy and potential energy.
View SolutionThe potential energy between two atoms in a molecule is given by U(x)=ax12−bx6, where a and b are positive constants and x is the distance between the atoms. The atom is in stable equilibrium when
View SolutionThe potential energy function for a diatomic molecule is U(x)=ax12−bx6. In stable equilibrium, the distance between the particles is .
View SolutionWhen the separation between two charges is increased, the electric potential energy of the charges
View SolutionWhen the separation between two charges is increased, the electric potential energy of the charges
View SolutionWhen the separation between two charges is increase the electric potential energy of the charges.
View SolutionThe graph showing the relation of the distance between two molecules with the inter molecular potential energy ( U ) is given in Figure. Find with the help of the graph.
(i) the distance between the molecule in their state of stable equilibrium.
(ii) the minimum and maximum distance between the molecules when the potential energy is −U1.
(iii) the energy required for the molecules to be free from each other when the distance between them is r2.
View Solution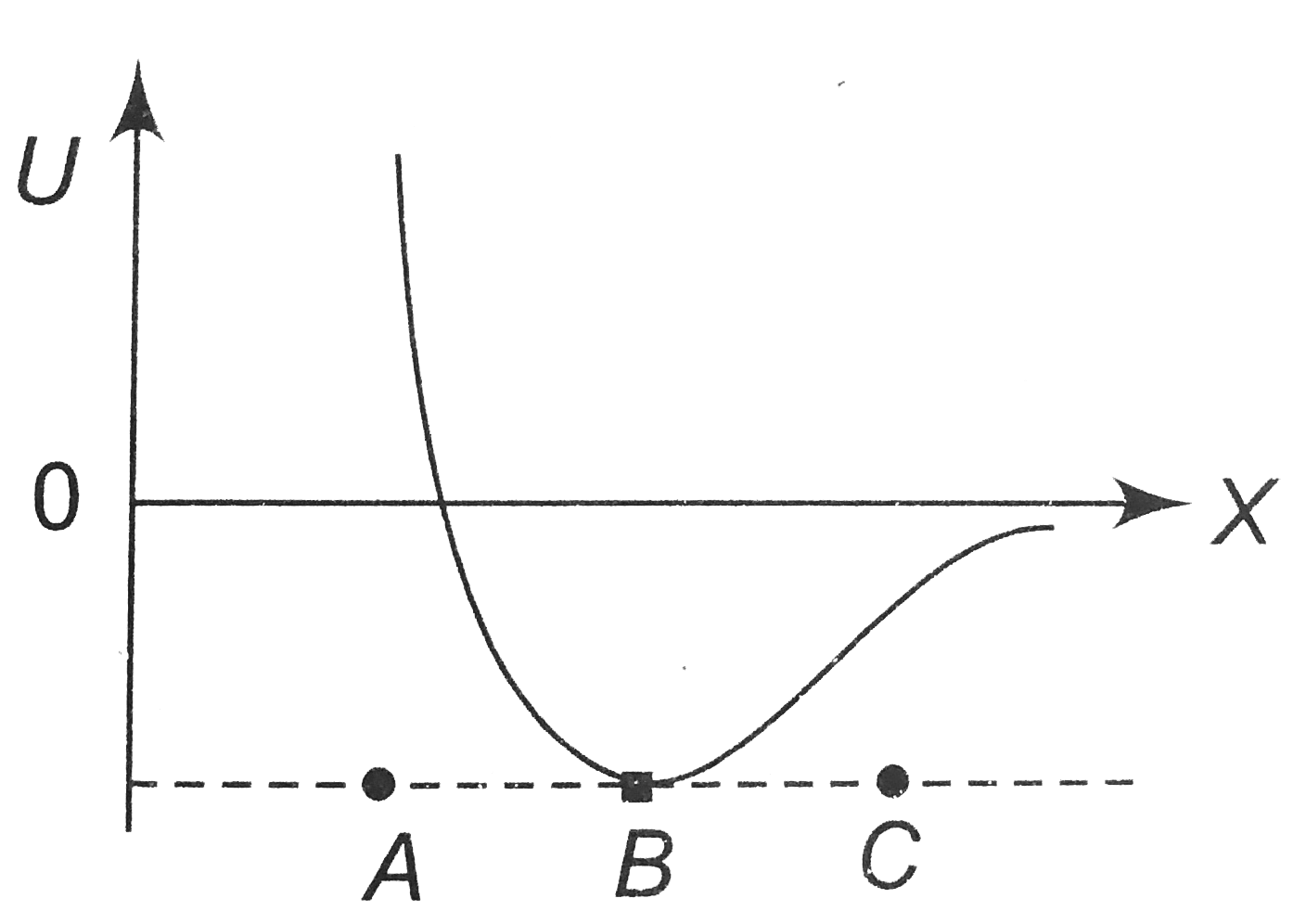
The potential energy U between two molecules as a function of the distance X between them has been shown in the figure. The two molecules are
View Solution
