A ball moving with a velocity of 6 m/s strikes an identical stationary ball. After collisions each ball moves at an angle of $30^{\circ}$ with the original line of motion. What are the speeds of the balls after the collision?

Text Solution

Verified by Experts

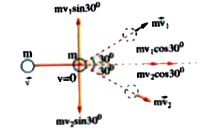
Applying the law of conservation of momentum perpendicular to the initial line of motion:
$0 = m v_{1} {sin 30}^{\circ} - m v_{2} {sin 30}^{\circ} or v_{1} = v_{2} \dots (i)$
Hence speed of both will be same after collision. Now along the line of motion:
$m v = m v_{1} {cos 30}^{\circ} + m v_{2} {cos 30}^{\circ} ... . . (i i)$
Putting equation (i) in equation (ii)
$m v = 2 m v_{1} {cos 30}^{\circ} (or) v_{1} = \frac{v}{\sqrt{3}} = \frac{6}{\sqrt{3}} = 2 \sqrt{3} m / s$

Updated on:21/07/2023

A ball moving with velocity of 6 m/s strikes an identical stationary ball. After collision each ball moves at an angle of $30^{\circ}$ with the original line of motion. What are the speeds of the balls after the collision ?
A $\frac{\sqrt{3}}{2} \frac{m}{sec}$
B $3 \frac{m}{sec}$
C $2 \sqrt{3} \frac{m}{sec}$
D $\sqrt{3} \frac{m}{sec}$
A ball moving with a velocity of 6 m/s strikes an identical stationary ball. After collision each ball moves at angle of $30^{\circ}$ with the original line of motion. Assuming that the collision is elastic, what are the speeds of the balls after the collision?
A $\frac{\sqrt{3}}{2} m / s, 2 \sqrt{3} m / s$
B $3 m / s, 2 \sqrt{3} m / s$
C $2 \sqrt{3} m / s, 2 \sqrt{3} m / s$
D $\sqrt{3} \frac{m}{s}, \sqrt{3} m / s$
A ball , moving with a speed of $10 \sqrt{3} m / s$ , strikes an identical stationary ball such that after the collision , the direction of each ball makes an angle of $30^{\circ}$ with the original line of motion. The speeds of two balla after the collision are , respectively.
A $5 m / s, 10 m / s$
B $10 m / s, 5 m / s$
C $5 m / s, 5 m / s$
D $10 m / s, 10 m / s$