A ball , moving with a speed of 10√3m/s , strikes an identical stationary ball such that after the collision , the direction of each ball makes an angle of 30∘with the original line of motion. The speeds of two balla after the collision are , respectively.
3ms−1,3ms−1
3√3ms−1,3√3ms−1
3√3ms−1,3ms−1
3ms−1,3√3ms−1
The correct Answer is:B
To solve the problem step by step, we will use the principles of conservation of momentum and the geometry of the collision.
Step 1: Understand the scenario
We have two identical balls. One ball is moving with a speed of 10√3m/s and strikes a stationary ball. After the collision, both balls move at an angle of 30∘ with respect to the original line of motion.
Step 2: Define the variables
Let:
- u1=10√3m/s (initial speed of the moving ball)
- u2=0m/s (initial speed of the stationary ball)
- v1 = speed of the first ball after the collision
- v2 = speed of the second ball after the collision
Step 3: Apply conservation of momentum
We will apply the conservation of momentum in both the x-direction and y-direction.
X-direction:
The initial momentum in the x-direction is:
mu1+mu2=m(10√3)+m(0)=m(10√3)
After the collision, the momentum in the x-direction is:
mv1cos(30∘)+mv2cos(30∘)
Setting these equal gives us:
m(10√3)=mv1cos(30∘)+mv2cos(30∘)
Cancelling m from both sides:
10√3=v1cos(30∘)+v2cos(30∘)
Y-direction:
The initial momentum in the y-direction is zero, since only the first ball is moving initially:
0=mv1sin(30∘)−mv2sin(30∘)
This simplifies to:
0=v1sin(30∘)−v2sin(30∘)
Thus, we find:
v1=v2
Step 4: Substitute v2 in the x-direction equation
Since v1=v2, we can substitute v2 with v1 in the x-direction equation:
10√3=v1cos(30∘)+v1cos(30∘)
This simplifies to:
10√3=2v1cos(30∘)
Using cos(30∘)=√32:
10√3=2v1(√32)
10√3=v1√3
Step 5: Solve for v1
Dividing both sides by √3:
v1=10m/s
Since v1=v2, we also have:
v2=10m/s
Final Answer:
The speeds of the two balls after the collision are:
- v1=10m/s
- v2=10m/s
We have two identical balls. One ball is moving with a speed of 10√3m/s and strikes a stationary ball. After the collision, both balls move at an angle of 30∘ with respect to the original line of motion.
Let:
- u1=10√3m/s (initial speed of the moving ball)
- u2=0m/s (initial speed of the stationary ball)
- v1 = speed of the first ball after the collision
- v2 = speed of the second ball after the collision
We will apply the conservation of momentum in both the x-direction and y-direction.
The initial momentum in the x-direction is:
mu1+mu2=m(10√3)+m(0)=m(10√3)
After the collision, the momentum in the x-direction is:
mv1cos(30∘)+mv2cos(30∘)
Setting these equal gives us:
m(10√3)=mv1cos(30∘)+mv2cos(30∘)
Cancelling m from both sides:
10√3=v1cos(30∘)+v2cos(30∘)
The initial momentum in the y-direction is zero, since only the first ball is moving initially:
0=mv1sin(30∘)−mv2sin(30∘)
This simplifies to:
0=v1sin(30∘)−v2sin(30∘)
Thus, we find:
v1=v2
Since v1=v2, we can substitute v2 with v1 in the x-direction equation:
10√3=v1cos(30∘)+v1cos(30∘)
This simplifies to:
10√3=2v1cos(30∘)
Using cos(30∘)=√32:
10√3=2v1(√32)
10√3=v1√3
Dividing both sides by √3:
v1=10m/s
Since v1=v2, we also have:
v2=10m/s
The speeds of the two balls after the collision are:
- v1=10m/s
- v2=10m/s
Topper's Solved these Questions
Similar Questions
A ball moving with a speed of 9ms−1 strikes an identical stationary ball such that after the collision the direction of each ball makes an angle of 30∘ with the original line of motion. The speeds of two balls after the collision is
View SolutionA billiard ball moving at a speed of 6.6 ms–1 strikes an identical stationary ball a glancingblow. After the collision, one ball is found to be moving at a speed of 3.3, ms–1 in a direction making an angle of 60º with the original line of motion. The velocity of the other ball is
View Solution
Knowledge Check
- Question 1 - Select One
A ball weighing 4 kg and moving with velocity of 8 m/sec. Collides with a stationary ball of mass 12 kg. After the collision, the two balls move together. The final velocity is
A0B2 m/secC8 m/secD16 m/sec
A ball of mass 1 kg moving with a velocity of 0.4 ms−1 collides with another stationary ball. After the collision, the first ball moves with a velocity of 0.3ms1 in a direction making an angle of 90∘ with its initial direction. The momentum of the second ball after the collision will be (in kg ms−1)
View SolutionA moving 2kg ball with a speed of 2ms−1 hits obliquely a stationary identical ball inelastically as shown. If the first ball move away with angle α=30∘ to the original path, find the total kinetic energy lost after the collision
 View Solution
View SolutionA ball A moving with a velocity 5 m/s collides elastically with another identical ball at rest such that the velocity of A makes an angle of 30∘ with the line joining the centres of the balls. Then consider following statements :
(A) Balls A an B move at right angles after collision
(B) kinetic energy is conserved
(C) speed of A after collision is (5/2) m/s
(D) speed of B after collision is (5√3/2) m/s
Select correct alternative :-View SolutionTwo identical billiard balls undergo an oblique elastic collision. Initially, one of the balls is stationary. If the initially stationary ball after collision moves in a direction which makes an angle of 37∘ with direction of initial motion of the moving ball, then the angle through which initially moving ball will be deflected is
View SolutionAn iron ball A collides with another stationary iron ball B If the ratio of radii of the balls is n = 2, find the ratio of their speeds just after the collision (e = 0.5)
 View Solution
View SolutionA ball of mass 5 kg moving with speed 8 m/s collides head on with another stationary ball of mass 15 kg. If collision is perfectly inelastic, then loss in kinetic energ is
View SolutionA highly elastic ball moving at a speed of 3m/s approaches a wall moving towards it with a speed of 3m/s. After the collision. the speed of the ball will be
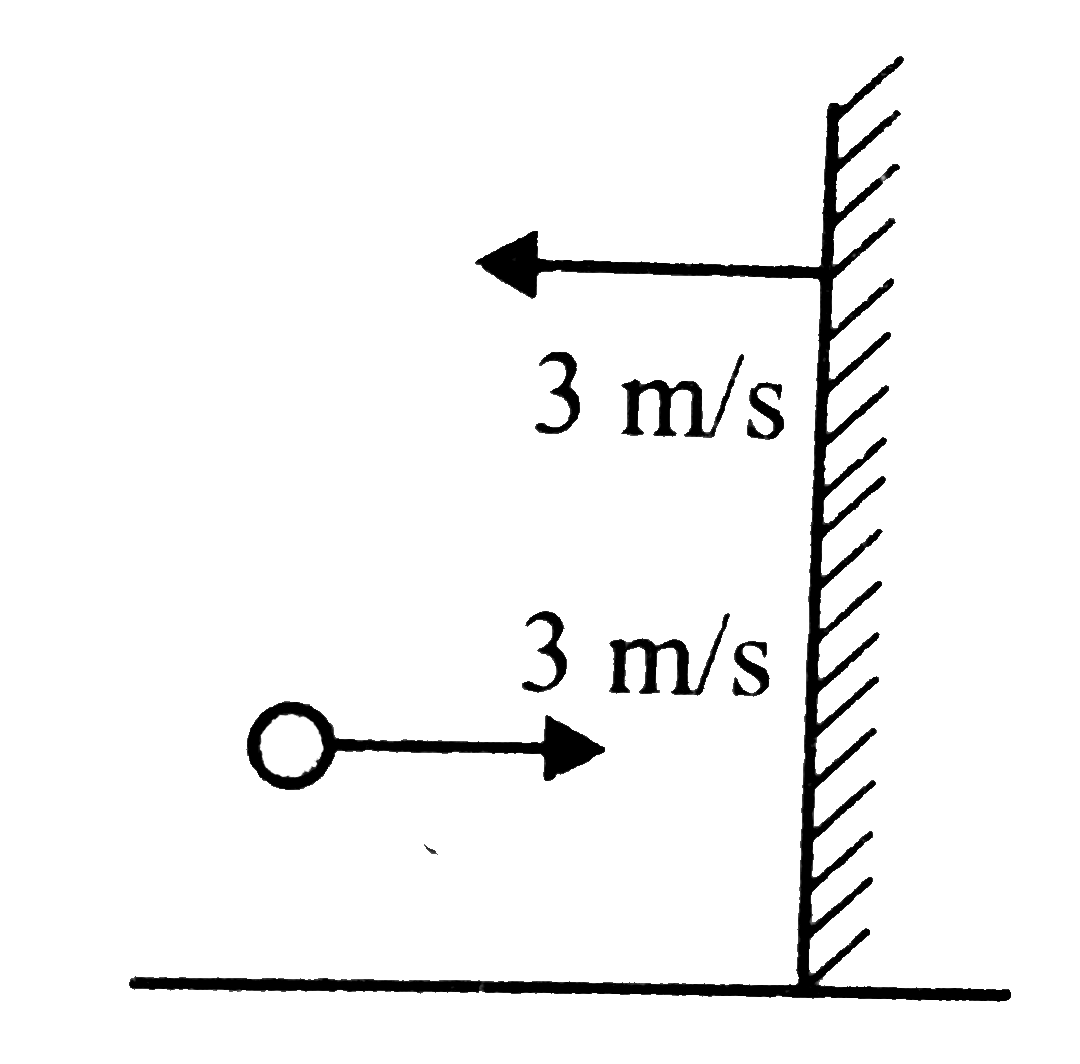 View Solution
View Solution

