Two particles A and B of equal mass m each are attached by a string of length 21 and initally placed over a smooth horizontal table in the position shown in figure Particle B is projected across the table with speed u perpendicular to AB as shown in figure. Find the velocities of the particles after the string becomes taut and the magnitude of the impulsive tension.
When the string beomes taut , both particles move with equal velocity component v in the directon AB.. Perpendicular to AB. there is no impulse on either particle, velocity components in this direction are therefore unchanged.
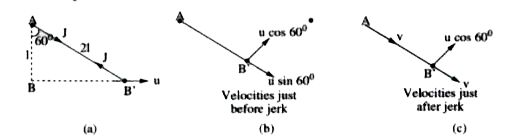
Using conservation of momentum in the direction AB..0+musin60∘=mv+mv
(or) v=√34u therefore, just after the jerk
(i) Velocity of mass A=√34u along AB.
(ii) Velocity of mass B=
⎷(ucos60∘)2+(√34u)2=√74u
in a direction inclined to AB. at an ange tan−1(ucos60∘v),i.e.,attan−1(2√3)
The magnitude of impulsive tension (J) can be calculated by considering the change of in momentum of one of the particles.
For the mass A, in the direction AB.,J=mv−0(or)J=√34mu
Topper's Solved these Questions
- COLLISIONS BOOK - AAKASH SERIESCHAPTER - COLLISIONS EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
12 Videos
- COLLISIONS BOOK - AAKASH SERIESCHAPTER - COLLISIONS EXERCISE - NUMERICAL EXERCISE ( LEVEL 1)
18 Videos
- CENTRE OF MASSBOOK - AAKASH SERIESCHAPTER - CENTRE OF MASSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED))
3 Videos
- ELASTICITYBOOK - AAKASH SERIESCHAPTER - ELASTICITYEXERCISE - Questions for Descriptive Answers
10 Videos
Similar Questions
Two particles A and B of equal mass m are attached by a string of length 2l and initially placed over a smooth horizontal table in the position shown in fig. particle B is projected across the table with speed u perpendicular to AB as shown in the figure. find the velocities of each particle after the string becomes taut and the magnitude of the impulse tension.
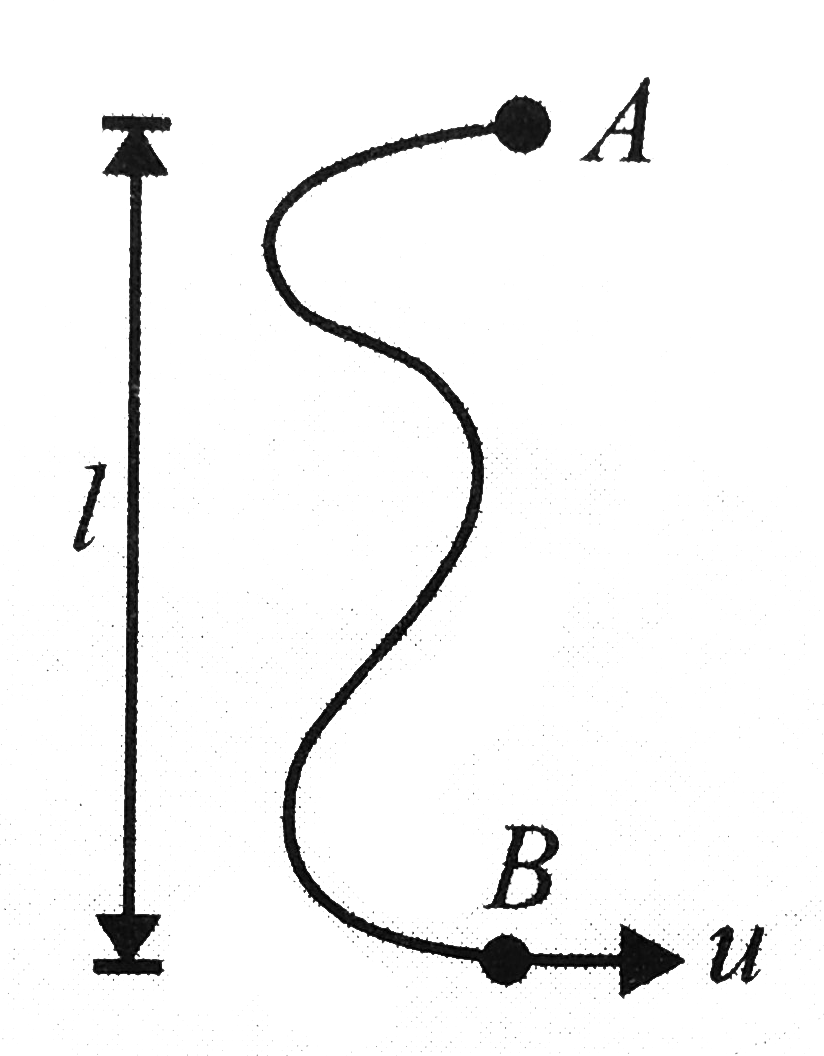
View SolutionTwo particles A and B of equal mass m are attached by a string of length 2l and initially placed over a smooth horizontal table in the positoin shown in fig. particle B is projected across the table with speed u perpendicular to AB as shown in the figure. find the velocities of each particle after the string becomes taut and the magnitude of the impulse tension.
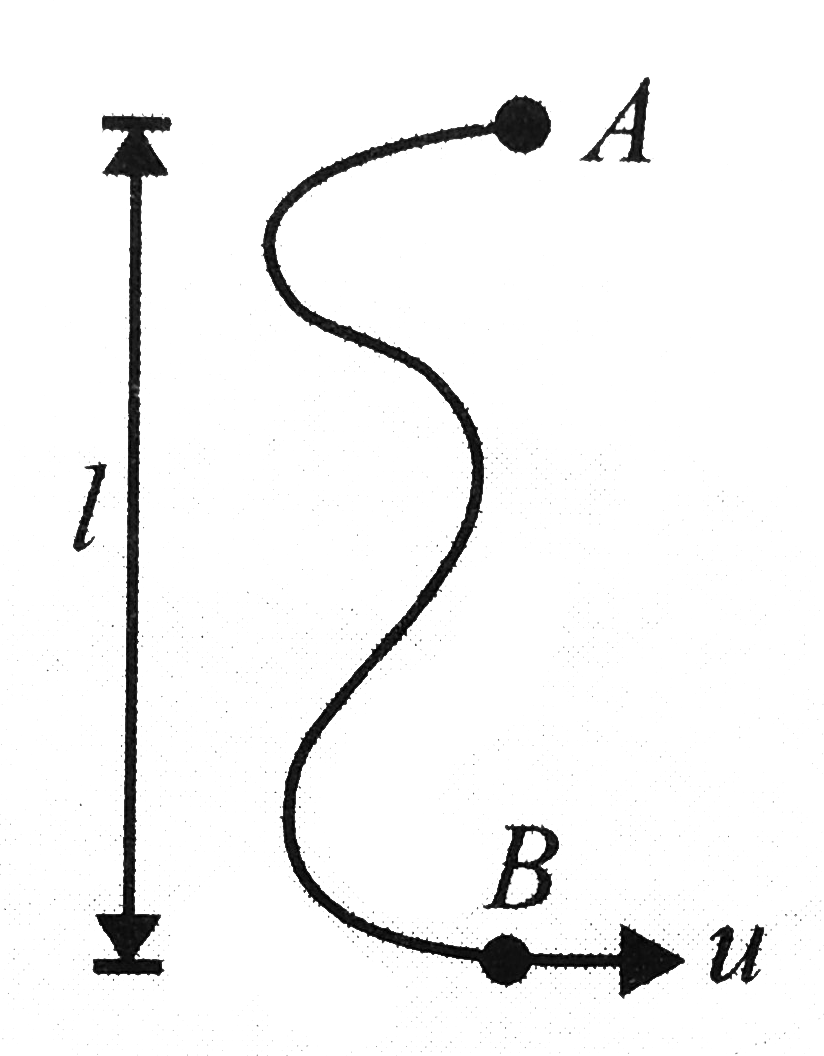
View SolutionTwo particles A and B of equal mass m are attached by a string of length 2l and initially placed over a smooth horizontal table in the positoin shown in fig. particle B is projected across the table with speed u perpendicular to AB as shown in the figure. find the velocities of each particle after the string becomes taut and the magnitude of the impulse tension.
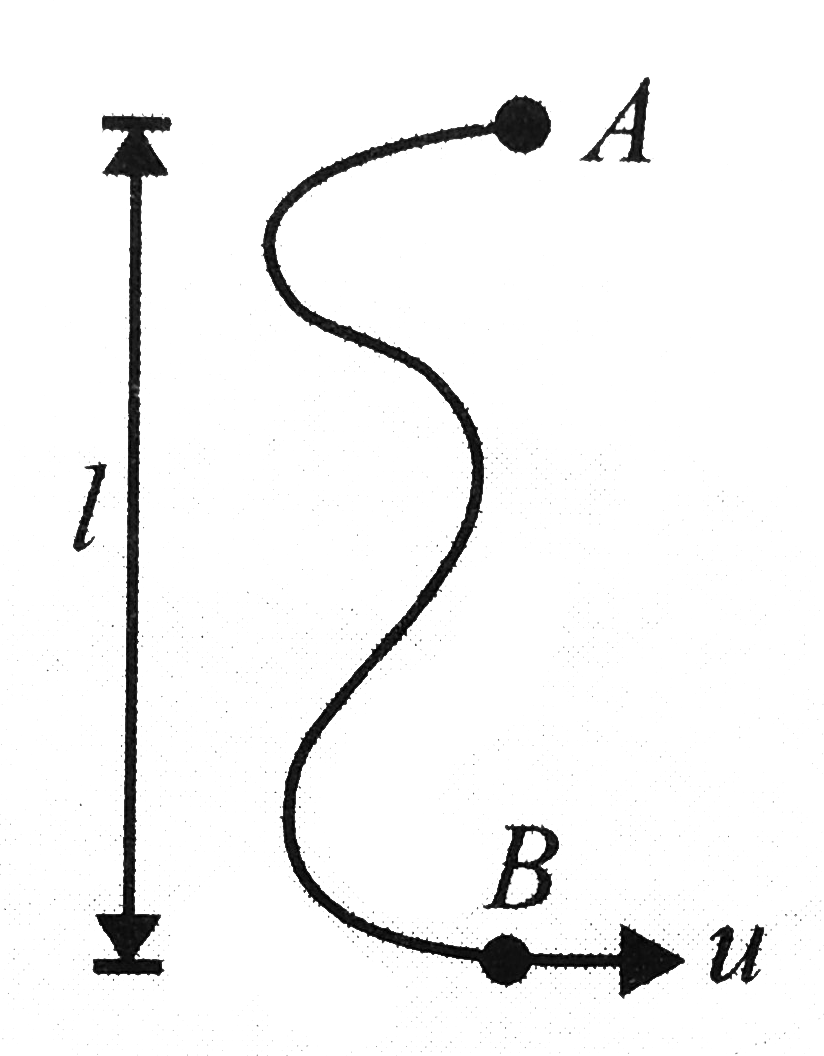
View SolutionTwo charged particles having charge 2.0×10−8C each are joined by an insulating string of length 1 m and the system is kept on a smooth horizontal table. Find the tension in the string.
View SolutionTwo charged particles having charge 2.0×10−8C each are joined by an insulating string of length 1 m and the system is kept on a smooth horizontal table. Find the tension in the string.
View SolutionTwo particles, each of m, are connected by a light inextensible string of length 2l. Initially they lie on a smooth horizontal table at points A and B distant l apart. The particle at A is projected across the table with velocity u. Find the speed with which the second particle begins to move if the direction of u is , (a) along BA, (b) at an angle of 120∘ with AB, (c) perpendicular to AB. In each case calculate (in terms of m and u) the impulse of tension in the string.
View SolutionTwo particles of mass m and 2m are connected by a string of length L and placed at rest over a smooth horizontal surface. The particles are then given velocities as indicated in the figure shown. The tension developed in the string will be

View SolutionTwo particles of mass m and 2m are connected by a string of length L and placed at rest over a smooth horizontal surface. The particles are then given velocities as indicated in the figure shown. The tension developed in the string will be

View SolutionTwo particles, each of mass m, are connected by a light inextensible string of lenthe 2l. Initially they lie on a smooth horizontal table at points A and B distant l apart. The particle at A is projected across the table with velocity u. Find the speed with which the second particle begins to move if the direction of u is :-
(i) along BA.
(ii) at an angle of 120∘ with AB
(iii) perpendicular to AB. In each case calculate (in teerms of m and u) the impulsive tension in the string.
View SolutionA particle of mass 1kg is attached to a string of length 5m. The string is attached to a fixed point O. It is released from the position as shown in Fig. Calculate
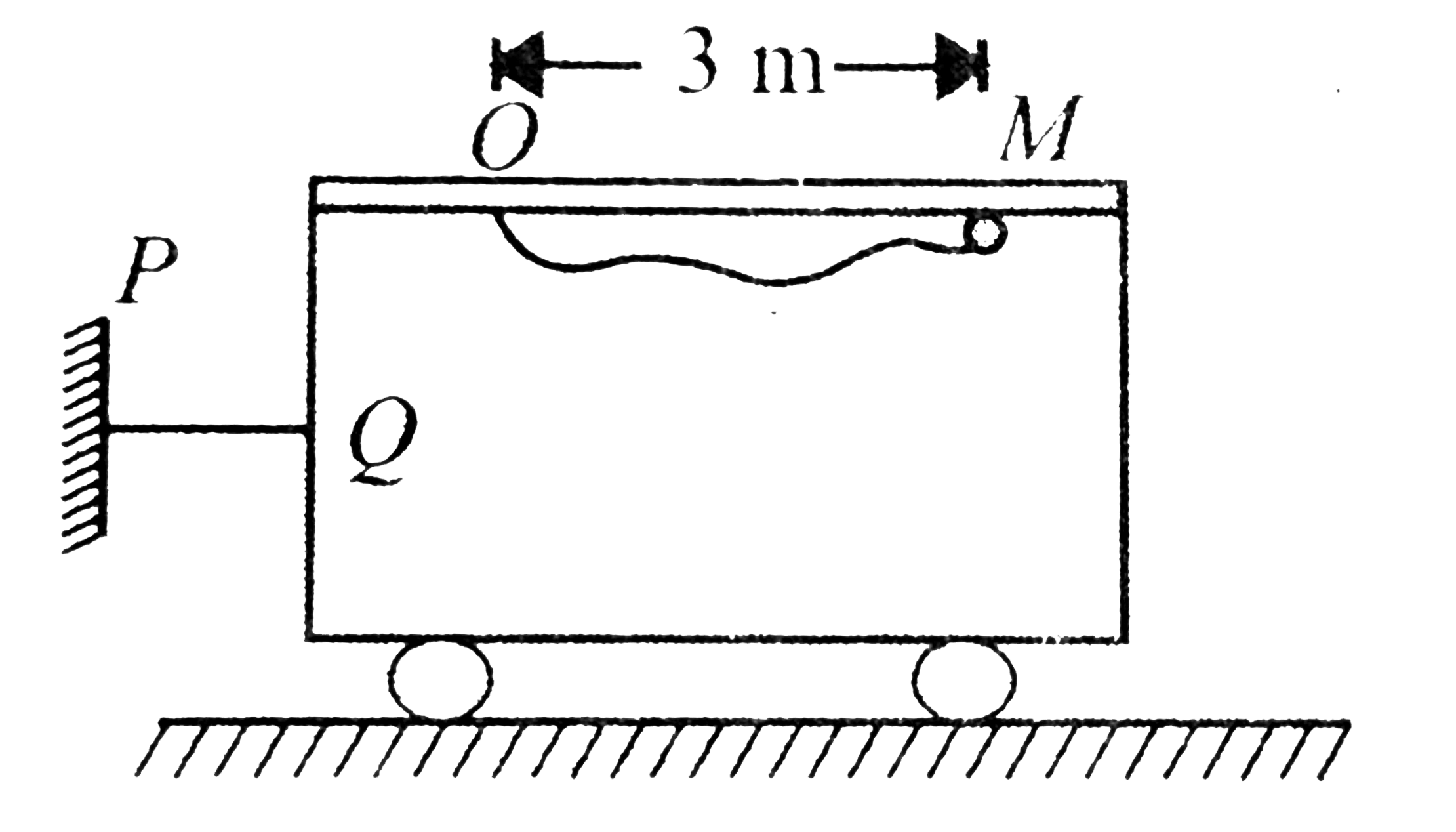
a. the impulse developed in the string when it becomes taut,
b. the velocity of the particle just after the string becomes taut,
c. the impulse developed in this string PQ at this instant.
View Solution
