Two particles, each of m, are connected by a light inextensible string of length 2l. Initially they lie on a smooth horizontal table at points A and B distant l apart. The particle at A is projected across the table with velocity u. Find the speed with which the second particle begins to move if the direction of u is , (a) along BA, (b) at an angle of 120∘ with AB, (c) perpendicular to AB. In each case calculate (in terms of m and u) the impulse of tension in the string.
The correct Answer is:(a)u/2,mu/2; (b) u√13/8,mu√13/8;(c)u√3/4,mu√3/4
(a) (##BSLPHYCMMCE01098_S01.png width=80%><br>ByconservationofmomentumrArrmv_(1)+mv_(1)=0+m u<br>rArr2mv_(1)=m u<br>rArrv_(1)=(u)/(2)<br>Imps–eoftension=chan≥∈momentumofpartic≤B<br>=mv_(1)-0=(m u)/(2)<br>(b)<imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/BSL_PHY_CMMC_E01_098_S02.pngwh=80%mx-autosty≤=background:white;>(justbeforeτt)<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/BSL_PHY_CMMC_E01_098_S03.pngwh=80%mx-autosty≤=background:white;>(justafterτt)<br>Bysinere–rArr(l)/(sintheta)=(2l)/(sin120^(@))rArrsintheta=(sqrt3)/(4)rArrcostheta=(sqrt(13))/(4)<br>Byconservationofmomentumalongthestr∈g<br>mv_(2)+mv_(2)=m(ucostheta)+m(0)<br>rArr" "v_(2)=(1)/(2)ucostheta=((1)/(2)u)((sqrt(13))/(4))=(sqrt(13))/(8)u<br>Imps–e=chan≥∈momentumofmassB<br>=m((sqrt(13))/(8)u)-0=(sqrt(13))/(8)m u<br>(c)<imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/BSL_PHY_CMMC_E01_098_S04.pngwh=80%mx-autosty≤=background:white;><br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/BSL_PHY_CMMC_E01_098_S05.pngwh=80%mx-autosty≤=background:white;><br>Byco≠rvationofmomentumalongthestr∈g<br>mv_(3)+mv_(3)=m(ucos30^(@))+0<br>rArrv_(3)=(1)/(2)ucos30^(@)=u(sqrt3)/(4)m u<br>Imps–e=chan≥∈momentumofmassB<br>=m(u(sqrt3)/(4))-0=(sqrt3)/(4)"mu"
Topper's Solved these Questions
- CENTRE OF MASS & MOMENTUM CONSERVATIONBook:BANSALChapter:CENTRE OF MASS & MOMENTUM CONSERVATIONExercise:EXERCISE-4 (SECTION-A) (JEE-ADVANCED Previous Year Questions)
Explore 11 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBook:BANSALChapter:CENTRE OF MASS & MOMENTUM CONSERVATIONExercise:EXERCISE-4 (SECTION-A) (Comprehension)
Explore 3 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBook:BANSALChapter:CENTRE OF MASS & MOMENTUM CONSERVATIONExercise:EXERCISE-2[MATRIX TYPE]
Explore 2 Videos
- GRAVITATIONBook:BANSALChapter:GRAVITATIONExercise:EXERCISE -4 Section - B
Explore 6 Videos
Similar Questions
Two particles, each of mass m, are connected by a light inextensible string of lenthe 2l. Initially they lie on a smooth horizontal table at points A and B distant l apart. The particle at A is projected across the table with velocity u. Find the speed with which the second particle begins to move if the direction of u is :-
(i) along BA.
(ii) at an angle of 120∘ with AB
(iii) perpendicular to AB. In each case calculate (in teerms of m and u) the impulsive tension in the string.
View SolutionTwo particle, each of mass m, are connected by a light inextensible string of length 2l. Initially they lie on a smooth horizontal table at points A ad B distant l apart the particle at A is projectd across the table with velocity u. find th speed with which the second particle begins to move if the direction. of u is :
(a). along BA
(b). at an angle of 120∘ with AB
(c) perpendicular to AB
In each case also calculate (in terms of ma nd u) the impulsive tension in the string.
View Solution
Knowledge Check
A heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-
A√31g,cos−1(3/2)B√1g3,cos−1(2/3)C√3g3,cos−1(2/3)D√gl3,cos−1(2/3)Two particle of equal mass m at A and B are connected by a rigid light rod AB lying on a smooth horizontal table. An impulse J is applied at A in the plane of the table and perpendicular at AB. The velocity of particle at A is
AJ2mBJmC2JmDzeroA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizonally with speed √gl . Find the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle.
A√glB√2glC√3glD√gl3
Two particles A and B of equal mass m are attached by a string of length 2l and initially placed over a smooth horizontal table in the positoin shown in fig. particle B is projected across the table with speed u perpendicular to AB as shown in the figure. find the velocities of each particle after the string becomes taut and the magnitude of the impulse tension.
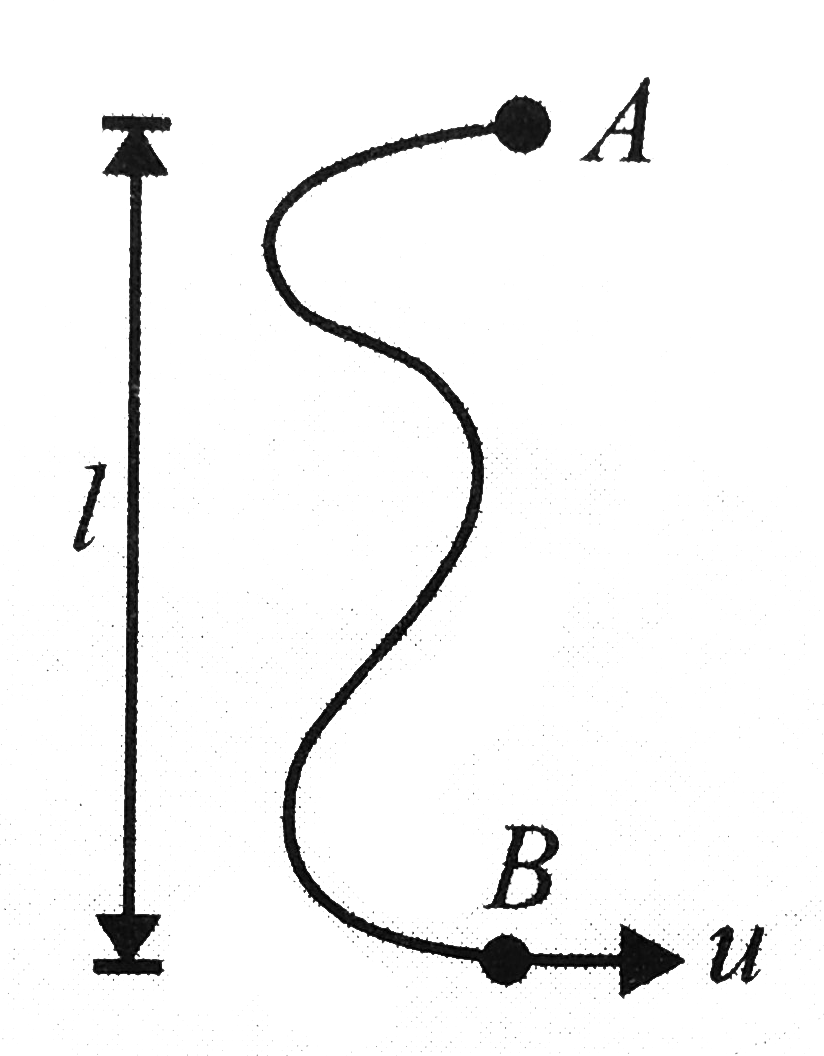
View SolutionTwo particles A and B of equal mass m are attached by a string of length 2l and initially placed over a smooth horizontal table in the position shown in fig. particle B is projected across the table with speed u perpendicular to AB as shown in the figure. find the velocities of each particle after the string becomes taut and the magnitude of the impulse tension.
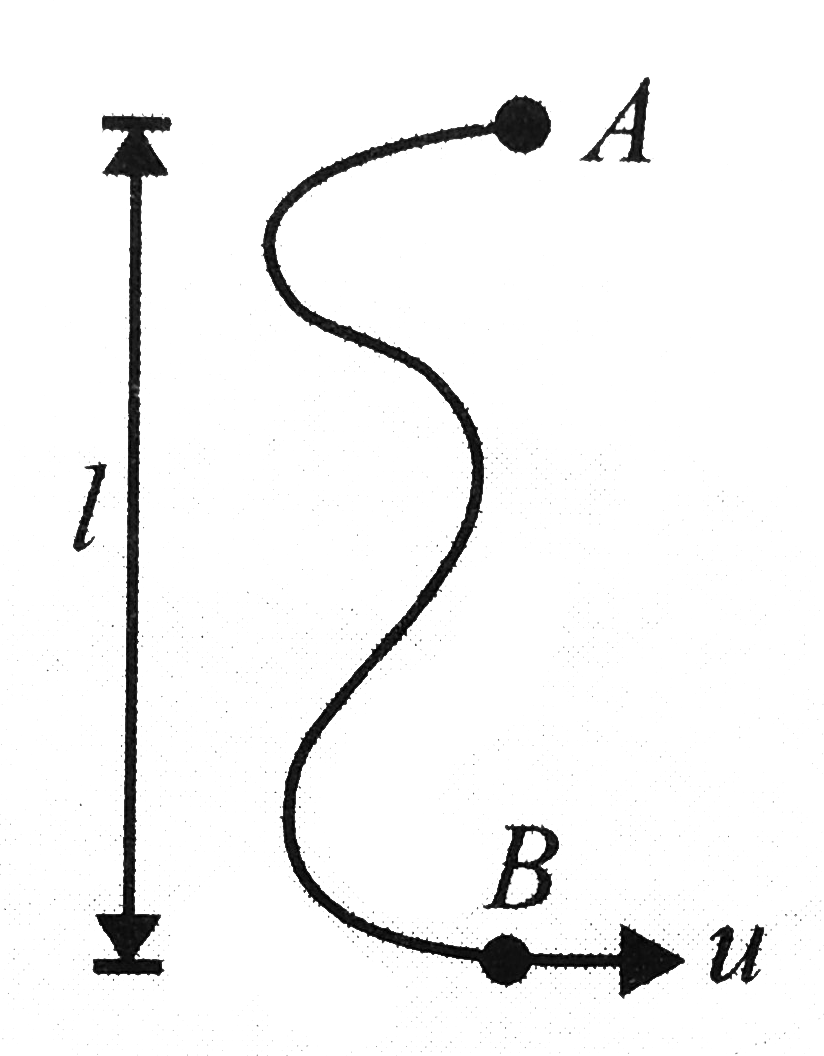
View SolutionTwo particles A and B of equal mass m are attached by a string of length 2l and initially placed over a smooth horizontal table in the positoin shown in fig. particle B is projected across the table with speed u perpendicular to AB as shown in the figure. find the velocities of each particle after the string becomes taut and the magnitude of the impulse tension.
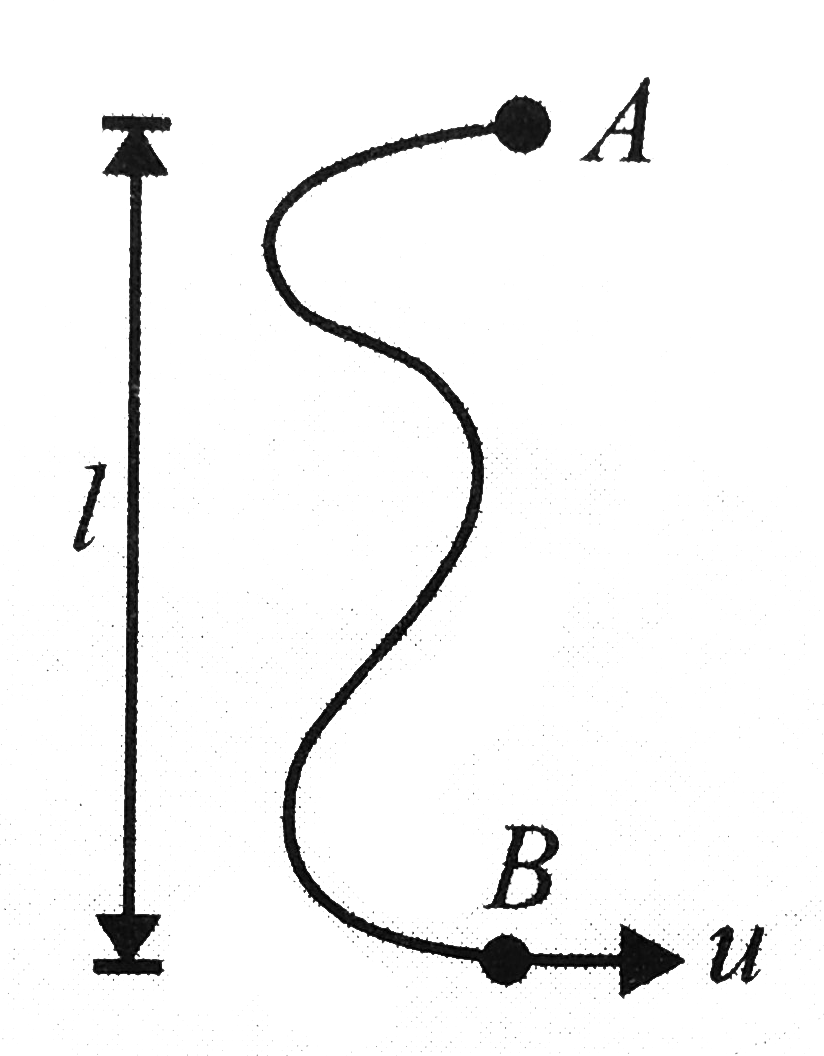
View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-
View SolutionTwo particles of mass m and 2m are connected by a string of length L and placed at rest over a smooth horizontal surface. The particles are then given velocities as indicated in the figure shown. The tension developed in the string will be

View Solution
