Find the centre of mass of the system:
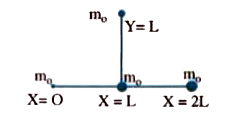
From the figure we can write,
Xcm=m0×0+m0×L+m0×L+m0×2Lm0+m0+m0+m0⇒Xcm=L
YCM=m0×0+m0×0+m0×L+m0×0m0+m0+m0+m0⇒Ycm=L4
∴ Co-ordinates of centre of mass are (Xcm,Ycm)=(L,L4)
Similar Questions
A cylindrical vessel of radius 1 m and height 2 m is half filled with water. Find the centre of mass of the system consisting of cylinder and water. The cylinder has mass 10 kg per square metre of it and density of water 1000 kg m−3.
View SolutionIf the system is released, then the acceleration of the centre of mass of the system :
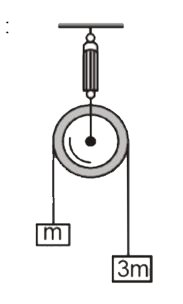
View Solution
Knowledge Check
If the system is released, then the acceleration of the centre of mass of the system is :
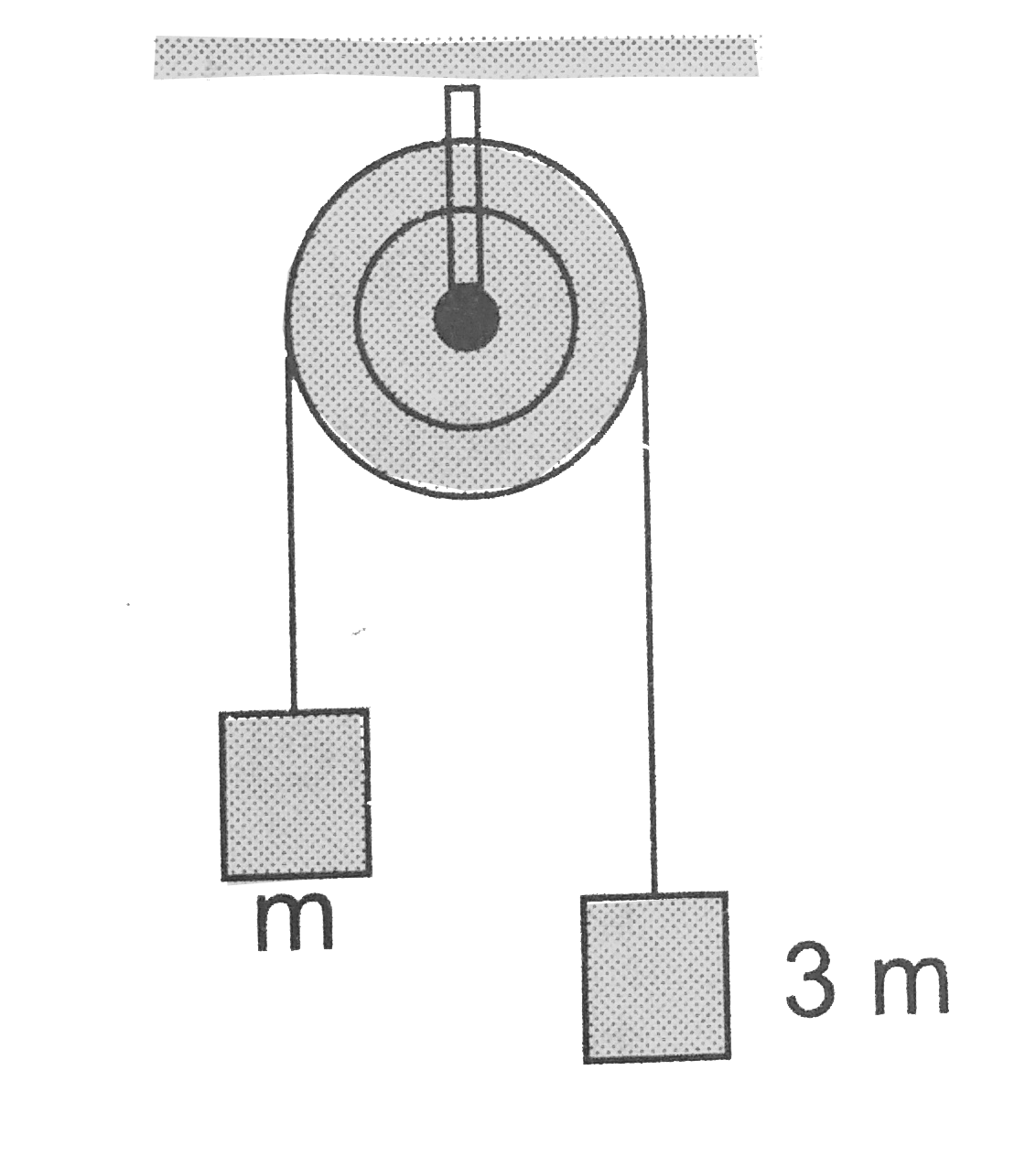 .Ag4Bg2CgD2 g
.Ag4Bg2CgD2 gIn the figure shown, find out centre of mass of a system of a uniform circular plate of radius 3R from O in which a hole of radius R is cut whose centre is at 2R distance from the centre of large circular plate
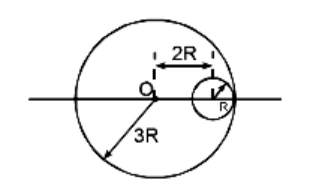 A(a) R2B(b) R5C(c) R4D(d) None of these
A(a) R2B(b) R5C(c) R4D(d) None of these
The coordinates of the positions of particles of mass 7, 4 and 10 gm are (1, 5,-3) , (2, 5, 7) and (3, 3,-1) respectively. Find the position of the centre of mass of the system?
View SolutionThe coordinates of the positions of particles of mass 7, 4 and 10 gm are (1, 5,-3) , (2, 5, 7) and (3, 3,-1) respectively. Find the position of the centre of mass of the system?
View SolutionFind out the centre of mass of a composite object shown in figure-4.28. Object consists of a cone with its base joint with the base of a hemisphere. The dimensions of the object are shown in figure. Assume uniform density of the system, find the centre of mass of this system.

View Solutionconsider there particles connected by massless rods. Find the locations fo the centre of mass of the system of three particles as shown in fig 4E.36

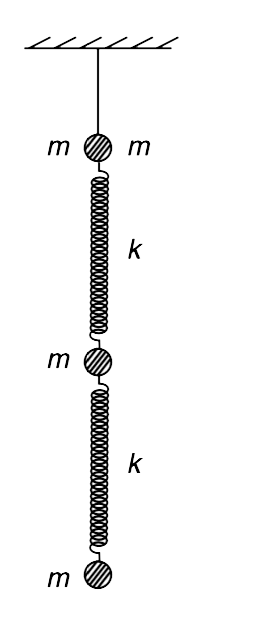
View SolutionThree small balls of equal mass (m) are suspended from a thread and two springs of same force constant (K) such that the distances between the first and the second ball and the second third ball are the same. Thus the centre of mass of the whole system coincides with the second ball. The thread supporting the upper ball is cut and system starts a free fall. Find the distance of the centre of mass of the system from the second ball when both the springs acquire their natural length in the falling system.
View SolutionIn the figure shown, find out centre of mass of a system of a uniform circular plate of radius 3R from O in which a hole of radius R is cut whose centre is at 2R distance from the centre of large circular plate

View Solution
