One end of a long metallic wire of length L is tied to the ceiling. The other end is tied to a spring of spring constant K. A mass m hangs from the free end of the spring. The area of cross-section and Young.s modulus of the wire are A and Y respectivley. Find the time period with which the mass m will oscillate if it is slightly pulled down and released?
Y=FA,Lx1⇒x1=FLAY,F=Kx2⇒x2=FK
x=x1+x2=F(LK+AY)KAY⇒x=ma(LK+AY)KAY,xam=(LK+AY)KAY⇒T=2π√xa
T=2π√m(LK+AY)KAY
Topper's Solved these Questions
- ELASTICITYBOOK - AAKASH SERIESCHAPTER - ELASTICITYEXERCISE - TEST YOUR SELF
11 Videos
- ELASTICITYBOOK - AAKASH SERIESCHAPTER - ELASTICITYEXERCISE - Very Short Answer Type Questions
15 Videos
- COLLISIONS BOOK - AAKASH SERIESCHAPTER - COLLISIONS EXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
4 Videos
- ELEMENTS OF VECTORS BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORS EXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWER
10 Videos
Similar Questions
One end of a long metallic wire of length (L) is tied to the ceiling. The other end is tied to a massless spring of spring constant . (K.A) mass (m) hangs freely from the free end of the spring. The area of cross- section and the Young's modulus of the wire are (A) and (Y) respectively. If the mass is slightly pulled down and released, it will oscillate with a time period (T) equal to :
View SolutionA mass m is attached to the free end of a massless spring of spring constant k with its other end fixed to a rigid support as shown in figure. Find out the time period of the mass, if it is displaced slightly by an amount x downward.
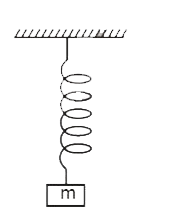
View Solution
Knowledge Check
One end of a long metallic wire of length (L) is tied to the ceiling. The other end is tied to a massless spring of spring constant . (K.A) mass (m) hangs freely from the free end of the spring. The area of cross- section and the Young's modulus of the wire are (A) and (Y) respectively. If the mass is slightly pulled down and released, it will oscillate with a time period (T) equal to :
A2π(m/K)1/2B2π√m((YA+KL))YAKC2π[(mYA/KL)1/2D2π[(mL/YA)1/2One end of a long mettalic wire of length L is tied to the ceiling. The other end is tied to massless spring of spring constant K. A mass M hangs freely from the free end of the spring. The area of cross-section and Young's modulus of the wire are A and Y respectively. If the mass is slightly pulled down and released, it will oscillate with a time period T equal to
A2π√(M/K)B2π√M(YA+KL)/YAKC2π√(MYA/KL)D√(ML/YA)A metal wire of length L, area of cross-section A and Young's modulus Y behaves as a spring of spring constant k.
Ak=YA/LBk=2YA/LCk=YA/2LDk=YL/A
A wire of length L,area of cross section A is hanging from a fixed support. The length of the wire changes to L1 when mass M is suspended from its free end. The expression for Young's modulus is:
View SolutionA wire of length L,area of cross section A is hanging from a fixed support. The length of the wire changes to L1 when mass M is suspended from its free end. The expression for Young's modulus is:
View SolutionIf a metal wire of length L, having area of cross-section A and young' s modulus Y . Behave as a spring of spring constant K. The value of K is
View SolutionIf a metal wire of length L, having area of cross-section A and Young's modulus Y, behaves as a spring constant K. The value of K is
View SolutionAn object of mass m, oscillating on the end of a spring with spring constant k has amplitude A. its maximum speed is
View Solution
