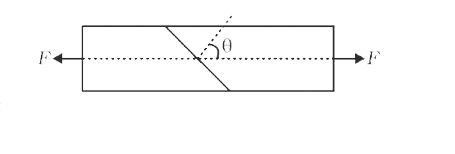
A bar of cross-section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angleθ with a plane at right angles to the bar.
By definition of bulk modulus, Bw=−VΔpΔV=−100×(100×1.013×105)(99.5−100)=2.026×109N/m2
Now as isothermal elasticity of a gas is equal to its pressure
BA=Eθ=p0=1.013×105N/m2
So that BWBA=CACW=2.026×1091.013×105=2×10 [ as C= compressibility 1B]
i.e., bulk modulus of water is very large as compared to air. This means that air is about 20,000 times more compressive than water, i.e., the average distance between air molecules is much larger than that between water molecules.
Topper's Solved these Questions
- ELASTICITYBOOK - AAKASH SERIESCHAPTER - ELASTICITYEXERCISE - TEST YOUR SELF
11 Videos
- ELASTICITYBOOK - AAKASH SERIESCHAPTER - ELASTICITYEXERCISE - Very Short Answer Type Questions
15 Videos
- COLLISIONS BOOK - AAKASH SERIESCHAPTER - COLLISIONS EXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
4 Videos
- ELEMENTS OF VECTORS BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORS EXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWER
10 Videos
Similar Questions
A bar of cross-section A is subjected to equal and opposite tensile forces at its ends. Consider a plane section of the bar whose normal makes an angle θ with the axis of the bar .
(i) What is the tensile stress on this plane?
(ii) What is the shearing stress on this plane?
(iii) For what value of θ is the tensile stress maximum
(iv) For what value of θ is the shearing stress maximum?
View SolutionA bar of cross-section A is subjected to equal and opposite tensile forces at its ends. Consider a plane section of the bar whose normal makes an angle θ with the axis of the bar .
(i) What is the tensile stress on this plane?
(ii) What is the shearing stress on this plane?
(iii) For what value of θ is the tensile stress maximum
(iv) For what value of θ is the shearing stress maximum?

View Solution
Knowledge Check
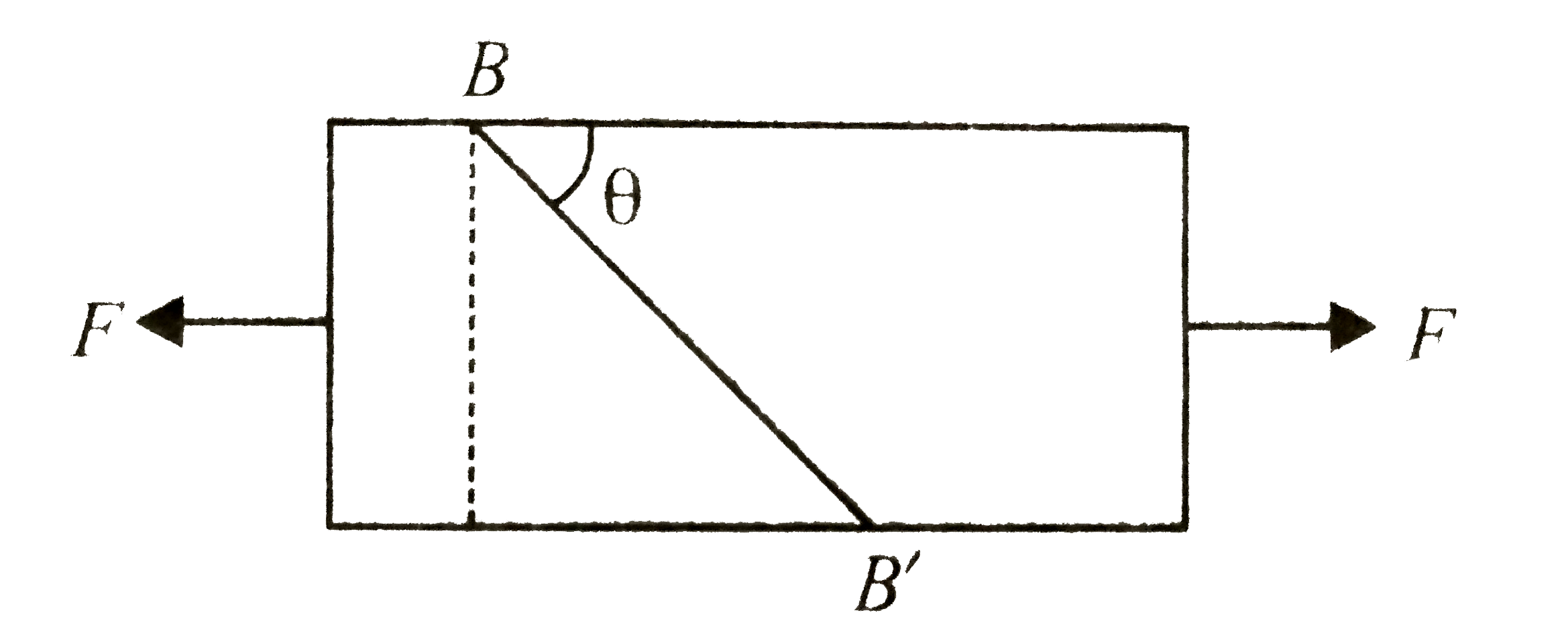
A bar of cross- sectional area A is is subjected two equal and opposite tensile forces at its ends as shown in figure. Consider a plane BB' making an angle θ with length
 AtanθBsecθCcotθDcosθ
AtanθBsecθCcotθDcosθA bar of cross- sectional area A is is subjected two equal and opposite tensile forces at its ends as shown in figure. Consider a plane BB' making an angle θ with length. The ratio of tensile stress to the shearing stress on the plane BB' is
 AtanθBsecθCcotθDcosθ
AtanθBsecθCcotθDcosθ
A bar of cross section A is subjected to equal and opposite tensile force at its ends. Consider a plane section of the bar whose normal makes an angle θ with the axis of the bar.

a. What is the tensile stress on the plane?
b. What is the shearing stress on the this plane?
c. For what value of θ is the tensile stress maximum?
d. For what value of θ is the shearing stress maximum?
View SolutionA bar of cross-section A is subjected two equal and opposite tensile forces at its ends consider a plane section of the bar whose makes an angle θ with the axis of the bar.
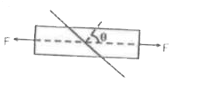
(a) what is the tensile stress on this plane ?
(b)what is the shearing stress on this plane ?
(c )for what value of θ is the tensile stress is maximum ?
(d) for what value of θ is the shearing stress maximum ?
View SolutionA bar of cross-section A is subjected two equal and opposite tensile forces at its ends consider a plane section of the bar whose makes an angle θ with the axis of the bar.

(a) what is the tensile stress on this plane ?
(b)what is the shearing stress on this plane ?
(c )for what value of θ is the tensile stress is maximum ?
(d) for what value of θ is the shearing stress maximum ?
View SolutionA bar of cross section A is subjected to equal and opposite tensile force at its ends. Consider a plane section of the bar whose normal makes an angle θ with the axis of the bar.

a. What is the tensile stress on the plane?
b. What is the shearing stress on the this plane?
c. For what value of θ is the tensile stress maximum?
d. For what value of θ is the shearing stress maximum?
View SolutionA steel bar of cross section A is subjected to two equal and opposite pulling forces at the two ends. If there is a plane through the bar making an angle α as shown, find

the shearing stress at this plane
View SolutionA steel bar of cross section A is subjected to two equal and opposite pulling forces at the two ends. If there is a plane through the bar making an angle α as shown, find

for what α the shearing strain is maximum.
View Solution
