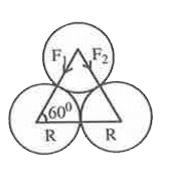
Three uniform spheres each having mass .m. and radius .r. are kept in such a way that each touches the other. The magnitude of the gravitational force on any sphere due to the other two is

Text Solution

Verified by Experts

Let $F_{1} = F_{2} = F$
Here $F = \frac{G m . m .}{{(2 R)}^{2}} = \frac{G m^{2}}{4 R^{2}}$
$∴$ The resultant gravitational force
$F_{R} = 2 F cos θ / 2$
$F_{R} = 2 F {cos 30}^{\circ} = \sqrt{3} F = \sqrt{3} \frac{G m^{2}}{{(2 R)}^{2}} = \sqrt{3} \frac{G m^{2}}{4 R^{2}}$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Three uniform spheres each of mass $m$ and diameter $D$ are kept in such a way that each touches the other two, then magnitudes of the gravitational force on any one sphere due to the other two is
A $\frac{3 G m^{2}}{D^{2}}$
B $\frac{2 \sqrt{3} G m^{2}}{D^{2}}$
C $\frac{\sqrt{3 G m^{2}}}{4 D^{2}}$
D $\frac{\sqrt{3} G m^{2}}{D^{2}}$
Question 2 - Select One
Three identical spheres, each having a charge q and radius R. are kept in such a way that each touches the other two. The magnitude of the electric force on any sphere due to the other two is
A $\frac{1}{4 π ε_{0}} {(\frac{q}{R})}^{2}$
B $\frac{\sqrt{3}}{4 π ε_{0}} {(\frac{q}{R})}^{2}$
C $\frac{\sqrt{3}}{16 π ε_{0}} {(\frac{q}{R})}^{2}$
D $\frac{\sqrt{5}}{16 π ε_{0}} {(\frac{q}{R})}^{2}$
Question 3 - Select One
Three uniform spheres, A, B and C each of mass M and radius R are kept in such a way that each sphere touches the other two. What is the magnitude of the gravitational force acting on A due to B and C ?
A $\frac{\sqrt{3} G M^{2}}{4 R^{2}}$
B $\frac{\sqrt{3} G M^{2}}{R^{2}}$
C $\frac{3 G M^{2}}{4 R^{2}}$
D $\frac{\sqrt{3} G M^{2}}{2 R}$

AAKASH SERIES-GRAVITATION-ADDITIONAL PRACTICE EXERCISE (LEVEL-II) PRACTICE SHEET (ADVANCED)Integer Type Questions

Home
Ask Doubt
Profile