F=Gm1m2r2 is valid
Between bodies with any shape
Between particles
Between any bodies with uniform density
Between any bodies with same shape
The correct Answer is:A
Topper's Solved these Questions
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - Exercise-II
78 Videos
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - Practice Exercise
56 Videos
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II) PRACTICE SHEET (ADVANCED)Integer Type Questions
6 Videos
- GAUSS.S LAW BOOK - AAKASH SERIESCHAPTER - GAUSS.S LAW EXERCISE - PROBLEMS (LEVEL - II)
12 Videos
- GRAVITATIONALBOOK - AAKASH SERIESCHAPTER - GRAVITATIONALEXERCISE - EXERCISE -3
154 Videos
Similar Questions
Knowledge Check
F=Gm1m2R2 is valid
ABetween bodies with any shapeBBetween particlesCBetween any bodies with uniform densityDBetween any bodies with same shapef−r2 is valid
Afor convex mirrors but not for concave mirrorsBfor concave mirrors but not for convex mirrorsCfor both convex and concave mirrorsDneither for convex mirrors nor for concave mirrors∫∞rGm1m2r2dr is equal to
AGm1m2rB−Gm1m2r3CGm1m2r3D−Gm1m2r
Find the dimensional formulae of the following quantities:
a. the universal constant of gravitation G,
b. the surface tension S,
c. the thermal conductivity k and
d. the coeficient of viscosity η.
Some equation involving these quantities are
F=Gm1m2r2,S=ρgrh2,
Q=kA(θ2−θ1)tdandF=−ρAv2−v1x2−x1
where the symbols have their usual meanings.
View SolutionFind the dimensional formulae of the following quantities:
a. the universal constant of gravitation G,
b. the surface tension S,
c. the thermal conductivity k and
d. the coeficient of viscosity η.
Some equation involving these quantities are
F=Gm1m2r2,S=ρgrh2,
Q=kA(θ2−θ1)tdandF=−ηAv2−v1x2−x1
where the symbols have their usual meanings.
View SolutionWrite proper answer in the box :
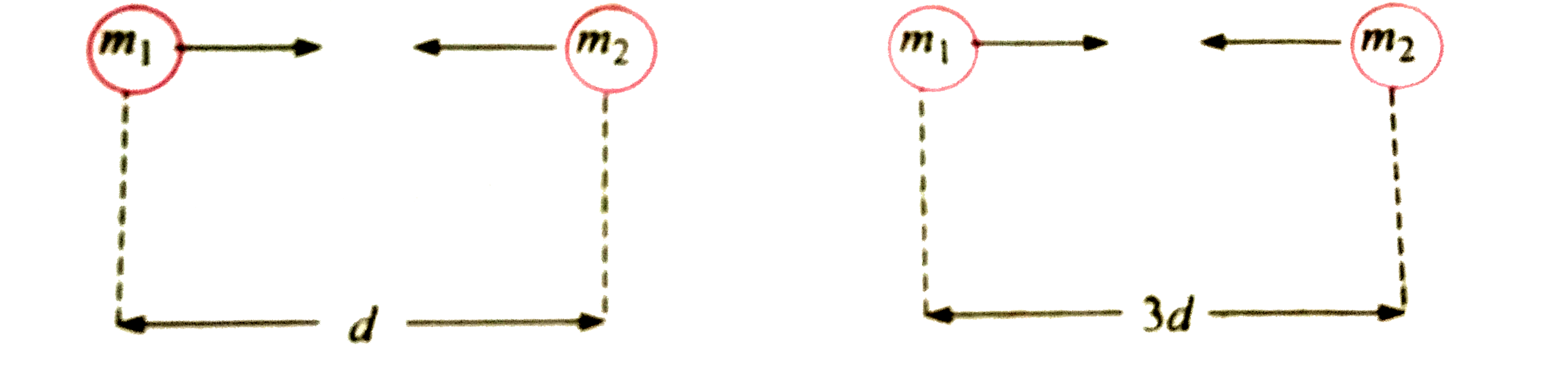
If F=Gm1m2d2 then F=
View SolutionAssertion : Mass of the rod AB is m1 and of particle P is m2. Distance between centre of rod and particle is r. Then the gravitational force between the rod and the particle is
F=Gm1m2r2
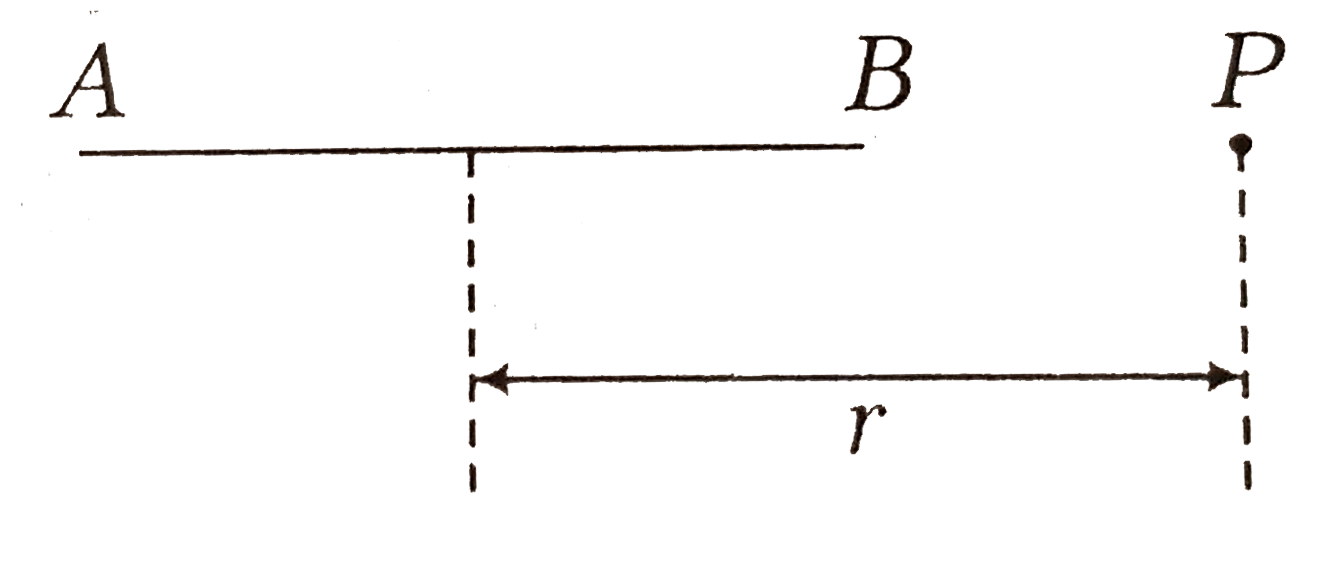
Reason : The relation F=Gm1m2r2 can be applied directly only to find force between two particles.
View SolutionWhich one of the following statements is true for the relation F=Gm1m2r2? (All symbols have their usual meanings)
View Solution
