A long rod ABC of mass "m" and length "L" has two particles of masses "m" and "2m" attached to it as shown in the figure. The system is initially in the horizontal position. The work to be done to keep it vertical with A at the bottom is (g = acceleration due to gravity)

2 mgl

$\frac{3 m g l}{2}$

$\frac{5 m g l}{2}$

3 mgl

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

A long rod $A B C$ of mass "m" and length "L" has two particles of masses "m" and "2m" attached to it as shown in the figure. The system is initially in the horizontal position. The work to be done to keep it vertical with $A$ hinged at the bottom is
.
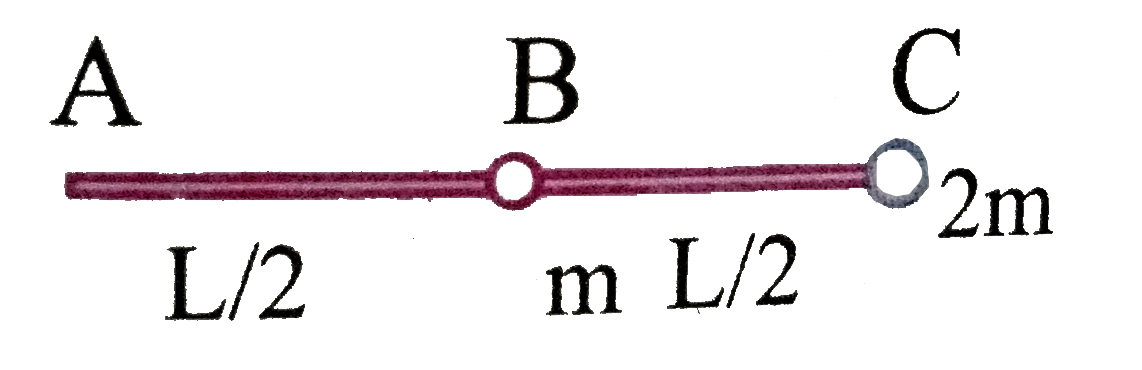A $2 m g L$
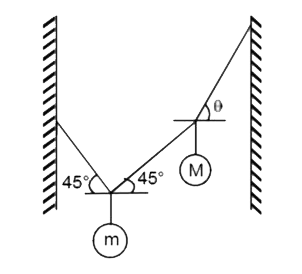
B $3 m g L / 2$
C $5 m g L / 2$
D $3 m g L$
Two masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then

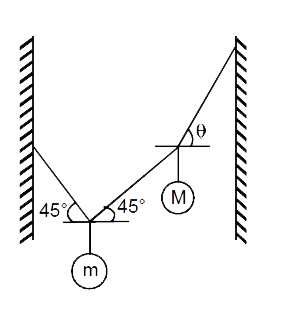A $tan θ = 1 + \frac{2 M}{m}$
B $tan θ = 1 + \frac{2 m}{M}$
C $cot θ = 1 + \frac{2 M}{m}$
D $cot θ = 1 + \frac{2 m}{M}$
A light rod of length $l$ has two masses $m_{1}$ and $m_{2}$ attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
A $(m_{1} + m_{2}) l^{2}$
B $\sqrt{m_{1} m_{2}} l^{2}$
C $\frac{m_{1} m_{2}}{m_{1} + m_{2}} l^{2}$
D $\frac{m_{1} + m_{2}}{m_{1} m_{2}} l^{2}$