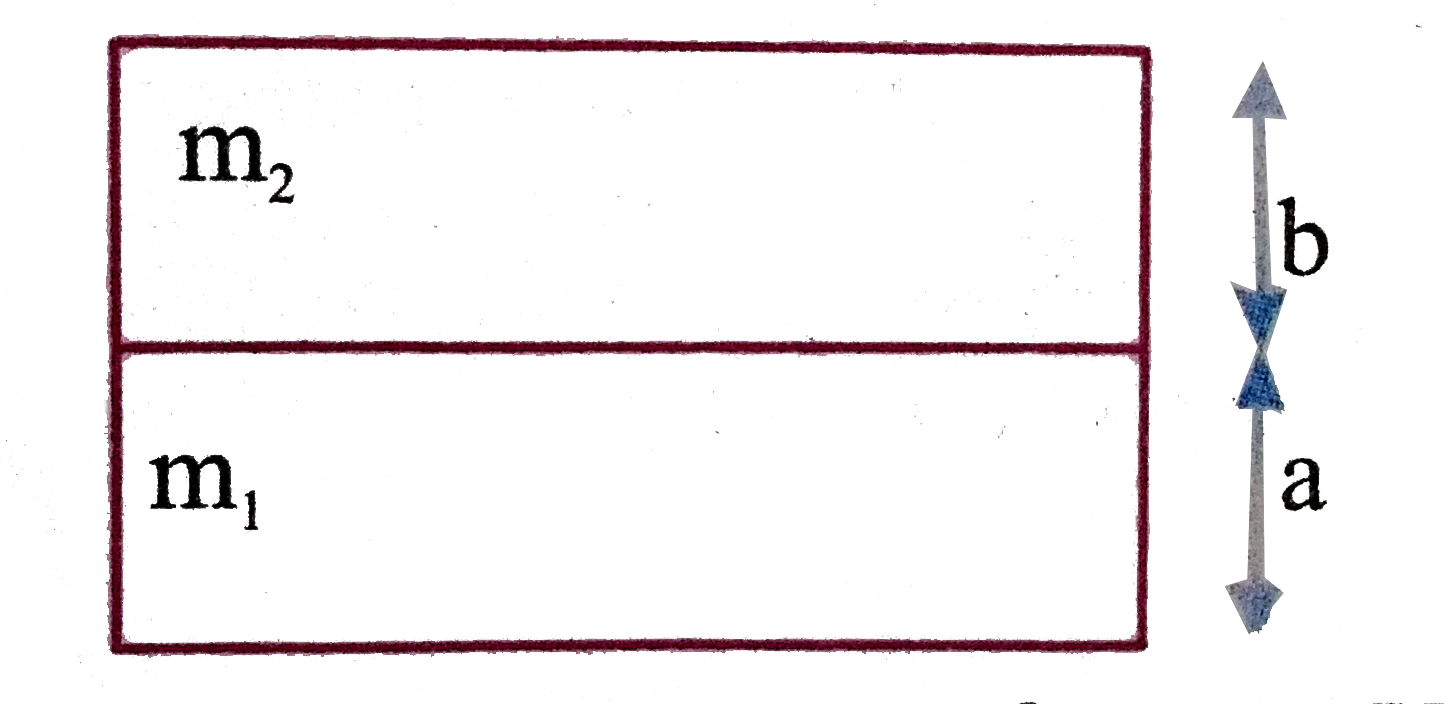
A rectangular plank of mass .m1.and height .a. is on a horizontal surface. On the top of it another rectangular plank of mass .m2. and height .b. is placed. The potential energy of the system is,
(m1+m2)a+b2g
[m1+m22.a+m2b2]g
[(m12+m2)a+m2b2]g
[(m12+m2)a+m1b2]g
The correct Answer is:C
Topper's Solved these Questions
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - WORK POWER ENERGY (SCALAR OR DOT PRODUCT) (POWER)
20 Videos
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - WORK POWER ENERGY (SCALAR OR DOT PRODUCT) (VERTICAL CIRCLE)
14 Videos
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - WORK POWER ENERGY (SCALAR OR DOT PRODUCT) (WORK)
33 Videos
- CALORIMETRY BOOK - AAKASH SERIESCHAPTER - CALORIMETRY EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) (LECTURE SHEET (ADVANCED)(Matrix Type Questions)
1 Videos
Similar Questions
A rectangular plank of mass m1 and height 'a' is on a horizontal surface. On the top of it another rectangular plank of mass m2 and height 'b' is placed. Find the potential energy of the system ?
 .
.
View SolutionA man of mass m is standing on a plank of equal mass m resting on a smooth horizontal surface. The man starts moving on the plank with speed u relative to the plank. The speed of the man relative to the ground is

View Solution
Knowledge Check
A man of mass m is standing on a plank of equal mass m resting on a smooth horizontal surface. The man starts moving on the plank with speed u relative to the plank. The speed of the man relative to the ground is
 A2uBu2CzeroDu4
A2uBu2CzeroDu4Block of mass m rests on the plank B of mass 3m which is free to slide on a frictionless horizontal surface. The coefficient of friction between the block and plank is 0.2. If a horizontal force of magnitude 2 mg is applied to the plank B, the acceleration of A relative to the plank and relative to the ground respectively, are
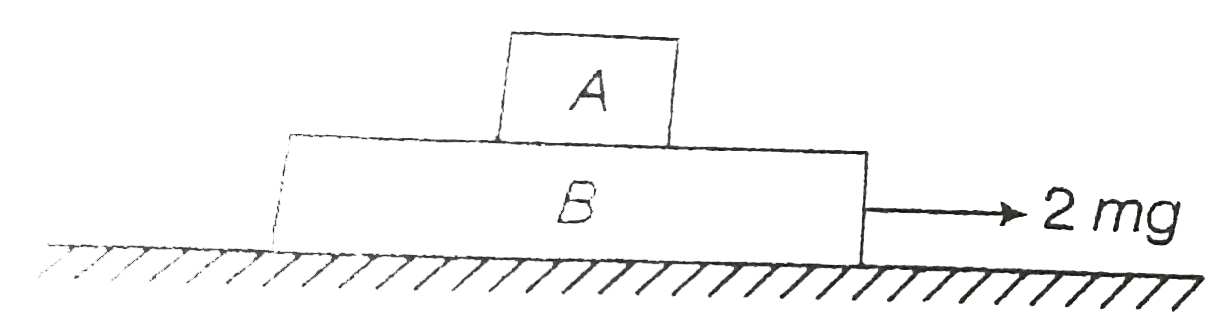 A0,(g),(2)B0,2g3C3g5,g5D2g5,g5
A0,(g),(2)B0,2g3C3g5,g5D2g5,g5A bar of mass m1 is placed on a plank of mass m2 which rests on a smooth horizontal plane . The coefficient of friction between the surfaces of bar and plank is k . The plank is subjected to a horizontal force F depending on time t as F = at , where a is a constant . The moment of time t0 at which the plank starts sliding is :
 Aakgm1+m2B(m1+m2)kgaC(m1+m2)gkaDka(m1+m2)g
Aakgm1+m2B(m1+m2)kgaC(m1+m2)gkaDka(m1+m2)g
Block A of mass m rests on the plank B of mass 3m which is free to slide on a frictionless horizo-ntal surface. The coefficient of friction between the block and plank is 0.2. If a horizontal force of magnitude 2 mg is applied to the plank B, the acceleration of A relative to the plank and relative to the ground respectively, are:

View SolutionIn the figure shown a plank of mass m is lying at rest on a smooth horizontal surface. A cylinder of same mass m and radius r is rotated to an angular speed w0 and then gently placed on the plank. It is found that by the time the slipping between the plank and the cylinder cease, 50% of total kinetic energy of the cylinder and plank system is lost. Assume that plank is long enough and um is the coefficient of friction between the cylinder and the plank.
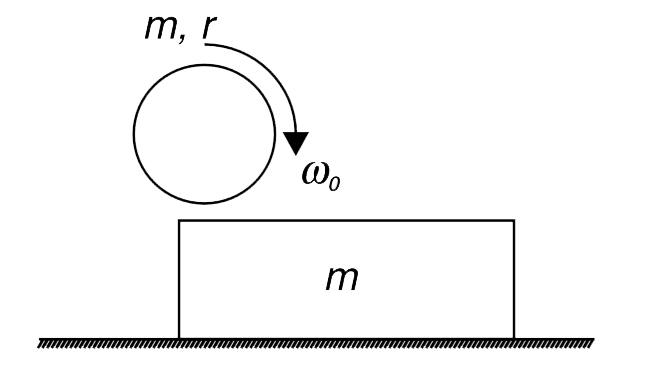
(a) Find the final velocity of the plank.
(b) Calculate the magnitude of the change in angular momentum of the cylinder about its centre of mass.
(c) Distance moved by the plank by the time slipping ceases between cylinder and plank.
View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionA uniform plank of mass m, free to move in the horizontal direction only , is placed at the top of a solid cylinder of mass 2m and radius R. The plank is attached to a fixed wall by mean of a light spring constant k. There is no slipping between the cylinder and the planck , and between the cylinder and the ground. Find the time period of small oscillation of the system.

View Solution
