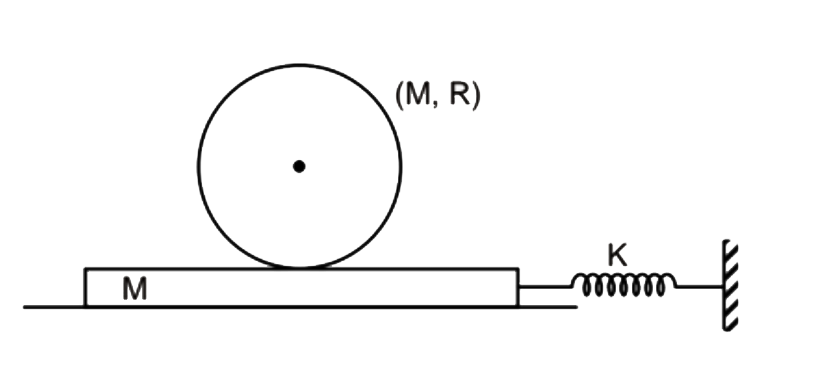
A uniform plank of mass m, free to move in the horizontal direction only , is placed at the top of a solid cylinder of mass $2 m$ and radius R. The plank is attached to a fixed wall by mean of a light spring constant k. There is no slipping between the cylinder and the planck , and between the cylinder and the ground. Find the time period of small oscillation of the system.

Video Solution

Text Solution

Verified by Experts

Method 1: When the plank is displaced slightly (say x) from equilibrium , as there is no sliding at any surface , the friction will be of static nature . As cylinder is rolling we can take the motion of the cylinder as pure rotation about point of contact.
Free body diagrams of plank and cylinder

Equation of motion for plank
$k x - f = m (a)$
Writing torque equation to cylinder about plank of contact
$f - (2 R) = i_{p} . α [\frac{1}{2} (2 m) R^{2} + 2 m R^{2}] α$
$= 3 m R^{2} α$
or $f = \frac{3}{2} m R a$
As cylinder is rolling we can write, the acceleration of topmost point of cylinder (or plank)
$a = α (2 R) \Rightarrow α R = \frac{a}{2}$
Substituting the value of (iii) and (ii), we get $f = \frac{3}{4} m a$
Now, from Eqs (i) and (iv),
$k x - (\frac{3}{4} m a) = m a$
$\Rightarrow a = \frac{4 k}{7 m} x$
Wtiting above equation with proper vector relation
$¯ a = - (\frac{4 k}{7 m}) ¯ x$
Comparing with stander equation $¯ a = - ω^{2} ¯ x$
which gives $ω^{2} = \frac{4 k}{7 m} or T = π \sqrt{\frac{7 m}{k}}$
Method 2: Suppose that the plank is displaced from its equilibrium position by x at time t , the center of the cylinder is therefore , displaced by $x / 2$ .
Therefore the mechanical energy of the system is given by
$E = K E (plank) + P E (spring) + K E (cylinder)$
$= \frac{1}{2} m v^{2} + \frac{1}{2} k x^{2} + \frac{1}{2} I_{p} ω^{2}$
$I_{P} = I_{G} + (2 m) R^{2} = \frac{1}{2} (2 m) R^{2} + (2 m) R^{2}$
$= 3 m R^{2}$
As cylinder is rolling velocity of center of cylinder will be half of the velocity of the plank (top most point of the cylinder)
$ν_{c y l \in d e r} = \frac{ν}{2} = ω R \Rightarrow ω = \frac{ν}{2 R}$
Substituting the value of $ω$ in Eq. (i) we get
$E = \frac{1}{2} m v^{2} + \frac{1}{2} k x^{2} + \frac{1}{2} (3 m R^{2}) (\frac{ν}{2 R})$
$= \frac{1}{2} m v^{2} + \frac{1}{2} k x^{2} + \frac{3}{8} m v^{2}$
$= \frac{7}{8} m v^{2} + \frac{1}{2} k x^{2}$
Differentiating Eq. (ii) w.r.t. time
$\frac{d E}{d t} = 0 = \frac{7}{8} m .2 v (\frac{d ν}{d t}) + k .2 x, (\frac{d x}{d t}$
$= \frac{7}{8} m ν . a + k x . ν$
Here $\frac{7}{4} m a + k x = 0 or a = - \frac{4 k}{7 m} x$
Comparing with $a = - ω^{2} x \Rightarrow T = 2 π \sqrt{\frac{7 m}{4 k}} = π \sqrt{\frac{7 m}{k}}$
Method 3: we can write Eq (ii)as $E = ν^{2} + \frac{4 k}{7 m} s^{2} =$ constant
as total energy of sysytem performing SHM is constant. Comparing with standard equation $ν^{2} + ω^{2} x^{2} = c o n s tan t$
which gives $ω^{2} = \frac{4 k}{7 m} or T = π \sqrt{\frac{7 m}{k}}$

Updated on:21/07/2023

|

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

A solid cylinder of mass $M$ and radius $R$ rolls without slipping down an inclined plane making an angle $6$ with the horizontal. Then its acceleration is.
A1/3 g sin $θ$
B2/3 g sin $θ$
C2/5 g sin $θ$
D2/7 g sin $θ$

CENGAGE PHYSICS ENGLISH-LINEAR AND ANGULAR SIMPLE HARMONIC MOTION-Solved Example

Home
Ask Doubt
Profile