In an elastic collision between two billiard balls. The variation of potential energy is represented by the graph (here r is the distance between centres of the balls and R is radius of the ball)
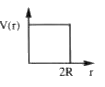
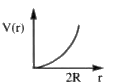
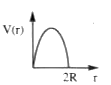
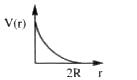
The correct Answer is:D
Topper's Solved these Questions
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - SYSTEM OF PARTICLES AND ROTATIONAL MOTION (CENTRE OF MASS)
36 Videos
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - SYSTEM OF PARTICLES AND ROTATIONAL MOTION (MOMENT OF INTERTIA)
18 Videos
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - WORK POWER ENERGY (SCALAR OR DOT PRODUCT) (VERTICAL CIRCLE)
14 Videos
- CALORIMETRY BOOK - AAKASH SERIESCHAPTER - CALORIMETRY EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) (LECTURE SHEET (ADVANCED)(Matrix Type Questions)
1 Videos
Similar Questions
In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the ball (i.e when they are in contact)?
View SolutionAnwer carefully, with reasons:
a) In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e. when they are in contact)?
Is the total linear momentum conserved during the short time of an elastic collision of two balls?
c) What are the answers to a) and b) for an inelastic collision?
d) If the potenital energy of two billiard balls depends only on the separation distance between their centers, is the collision elastic or inelastic? (note we are talking here of potential energy corresponding to the force during collision, not gravitational potential energy).
View Solution
Knowledge Check
In an elastic collision between smooth balls :
AThe kinetic energy remain constantBThe linear momentum remains constantCThe final kinetic energy is equal to the initial kinetic energyDThe final linear momentum is equal to the initial linear momentumIn an elastic collision of two billiard balls which of the following quantities is not conserved during the short time of collision :
AMomentumBTotal mechanical energyCKinetic energyDNoneAssertion: Collisionn between two billiard's ball are inelastic
Reason: Momentum remains conserve during the collision.A1. If both assertion and reason are true and reason is the correct explanation of assertion.B2. If both assertion and reson are true but reason is not the correct explanation of assertion.C3. if assertion is true but reason is false.D4. If both assertion and reason are false.
Anwer carefully, with reasons:
a) In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e. when they are in contact)?
Is the total linear momentum conserved during the short time of an elastic collision of two balls?
c) What are the answers to a) and b) for an inelastic collision?
d) If the potenital energy of two billiard balls depends only on the separation distance between their centers, is the collision elastic or inelastic? (note we are talking here of potential energy corresponding to the force during collision, not gravitational potential energy).
View SolutionAnwer carefully, with reasons:
a) In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e. when they are in contact)?
Is the total linear momentum conserved during the short time of an elastic collision of two balls?
c) What are the answers to a) and b) for an inelastic collision?
d) If the potenital energy of two billiard balls depends only on the separation distance between their centers, is the collision elastic or inelastic? (note we are talking here of potential energy corresponding to the force during collision, not gravitational potential energy).
View SolutionAssertion: Collisionn between two billiard's ball are inelastic
Reason: Momentum remains conserve during the collision.
View SolutionA smooth tunnel is dug along the radius of earth that ends at centre. A ball is relrased from the surface of earth along tunnel. Caefficient of restitution for collision between soil at centre and ball is 0.5. Caculate the distance travelled by ball just second collision at center. Given mass of the earth is M and radius of the earth is R.
View SolutionA smooth tunnel is dug along the radius of earth that ends at centre. A ball is relrased from the surface of earth along tunnel. Caefficient of restitution for collision between soil at centre and ball is 0.5. Caculate the distance travelled by ball just second collision at center. Given mass of the earth is M and radius of the earth is R.
View Solution
