A ball of mass m moving with a horizontal velocity v strikes the bob of the pendulum at rest. Moss of the bob of the pendulum is also m. During this collision the ball sticks with the bob. The height to which the combined mass rises (g=acceleration due to gravity)
v24g
v28g
v2g
v22g
The correct Answer is:B
Topper's Solved these Questions
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - SYSTEM OF PARTICLES AND ROTATIONAL MOTION (CENTRE OF MASS)
36 Videos
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - SYSTEM OF PARTICLES AND ROTATIONAL MOTION (MOMENT OF INTERTIA)
18 Videos
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - WORK POWER ENERGY (SCALAR OR DOT PRODUCT) (VERTICAL CIRCLE)
14 Videos
- CALORIMETRY BOOK - AAKASH SERIESCHAPTER - CALORIMETRY EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) (LECTURE SHEET (ADVANCED)(Matrix Type Questions)
1 Videos
Similar Questions
A ball of mass 'm' moving with a horizontal velocity 'v' strikes the bob of mass 'm' of a pendulum at rest. During this collision, the ball sticks with the bob of the pendulum. The height to which the combined mass raises is (g = acceleration due to gravity).
View SolutionA ball of mass m moving horizontally at a speed v collides with the bob of a simple pendulum at rest. The mass of the bob is also m. If the collision is perfectly elastic and both balls sticks, the height to which the two balls rise after the collision will be given by:
View Solution
Knowledge Check
A ball of mass 'm' moving with a horizontal velocity 'v' strikes the bob of mass 'm' of a pendulum at rest. During this collision, the ball sticks with the bob of the pendulum. The height to which the combined mass raises is (g = acceleration due to gravity).
Av24gBv28gCv2gDv22gA ball of mass m moving horizontally at a speed v collides with the bob of a simple pendulum at rest. The mass of the bob is also m. If the collision is perfectly inelastic and both balls sticks, the height to which the two balls rise after the collision will be given by:
Av2gBv22gCv24gDv28gA particle of mass m moving with velocity V0stick a simple pendulum of mass m and stick to it. The maximum height attained by the pendulum will be
Ah=V208gB√V0gC2√V0gDV204g
Derive an expression for the time period (T) of a simple pendulum which may depend upon the mass (m) of the bob, length (l) of the pendulum and acceleration due to gravity (g).
View SolutionA small ball of mass m moving with speed v collides elastically with a simple pendulum with bob of mass m at rest. The maximum height attained by the bob after collision is
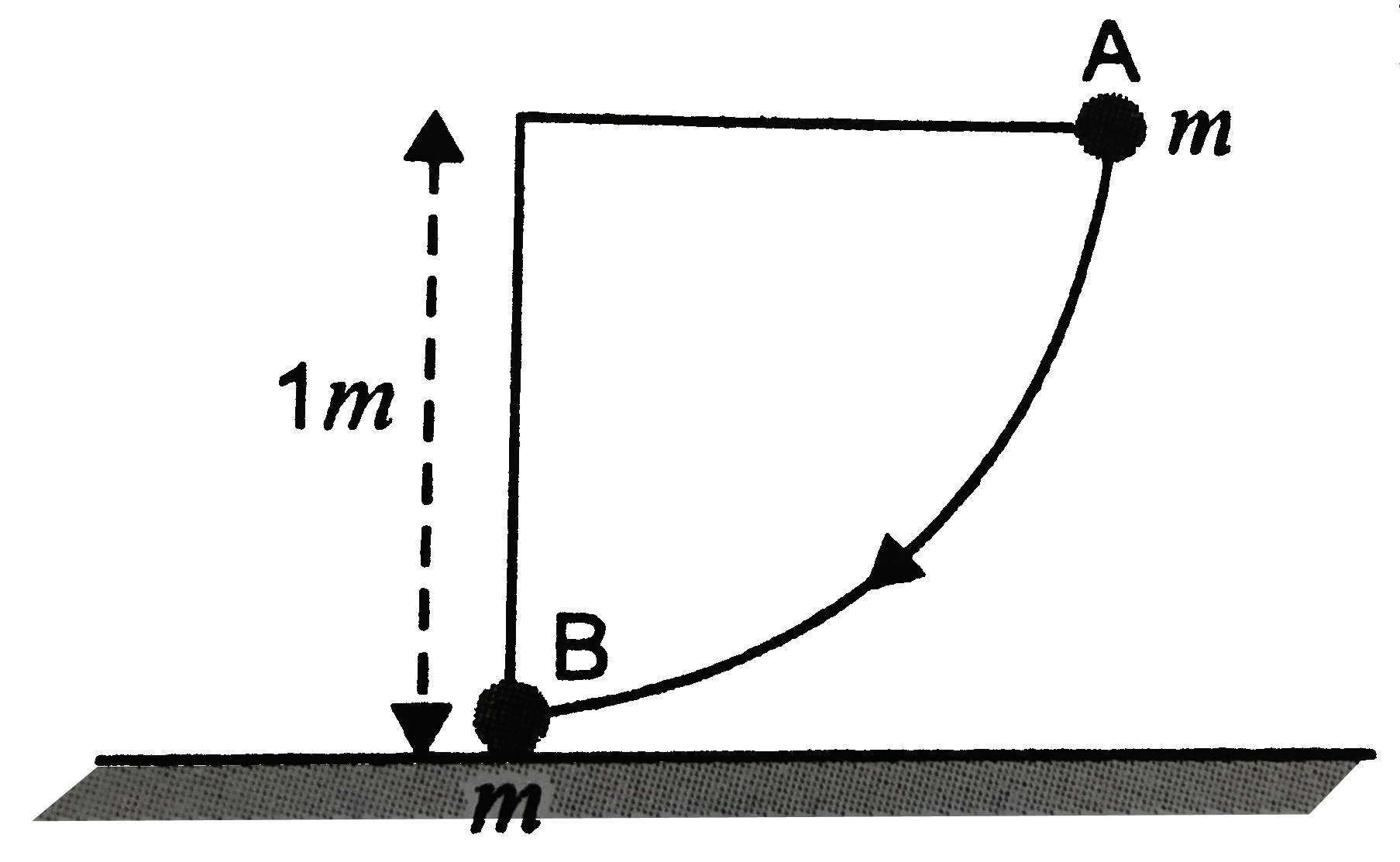
View SolutionThe bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
If the length of the pendulum is 1m, calculate
(a) the height to which bob A will rise after collision.
(b) the speed with which bob B starts moving.
Neglect the size of the bobs and assume the collision to be elastic.
View SolutionA particle of mass m moving with velocity V0 strikes a simple pendulum of mass m and sticks to it. The maximum height attained by the pendulum will be
View SolutionIf 'V' be the maximum velocity of the bob of a pendulum and 'h' the maximum height of the bob from its point of rest, then
View Solution
