On a large tray of mass M an ice cube of mass m, edge L is kept. If the ice melts completely, the centre of mass of the system come down by
mL2(M+m)
(M−m)L2(M+m)
(M+2m)L2(M+m)
2MLM+m
The correct Answer is:A
Topper's Solved these Questions
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - SYSTEM OF PARTICLES AND ROTATIONAL MOTION (MOMENT OF INTERTIA)
18 Videos
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - SYSTEM OF PARTICLES AND ROTATIONAL MOTION (CONSERVATION OF ANGULAR MOMENTUM)
7 Videos
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - WORK POWER ENERGY (SCALAR OR DOT PRODUCT) (COLLISIONS)
26 Videos
- CALORIMETRY BOOK - AAKASH SERIESCHAPTER - CALORIMETRY EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) (LECTURE SHEET (ADVANCED)(Matrix Type Questions)
1 Videos
Similar Questions
A cubical block of ice of mass m and edge L is placed in a large tray of mass M. If the ice melts, how far does the centre of mass of the system ''ice plus tray'' come down?
View SolutionA cubical block of ice of mass m and edge L is placed in a large tray of mass M. If the ice melts, how far does the centre of mass of the system ''ice plus tray'' come down?
View Solution
Knowledge Check
Two point masses m and M are separated bya distance L . The distance of the centre of mass of the system from m is
AL(m/M)BL(M/m)CL(Mm+M)DL(mm+M)Two point masses m and M are separated by a distance L . The distance of the centre of mass of the system from m is
AL(m/M)BL(M/m)CL(Mm+M)DL(mm+M)Three particles each of mass m are arranged at the corners of an equililateral triangle of side L. If one of masses is doubled. The shift in the centre of mass of the system
AL√3BL4√3C√3L4DL2√3
Consider a gravity free hall in which a tray of mas M, carrying a cubical block of icce of mas m and edge L, is at rest in the middle.. If the ice melts, by what distnce does the centre of mass of the tray plus the ice system descend?
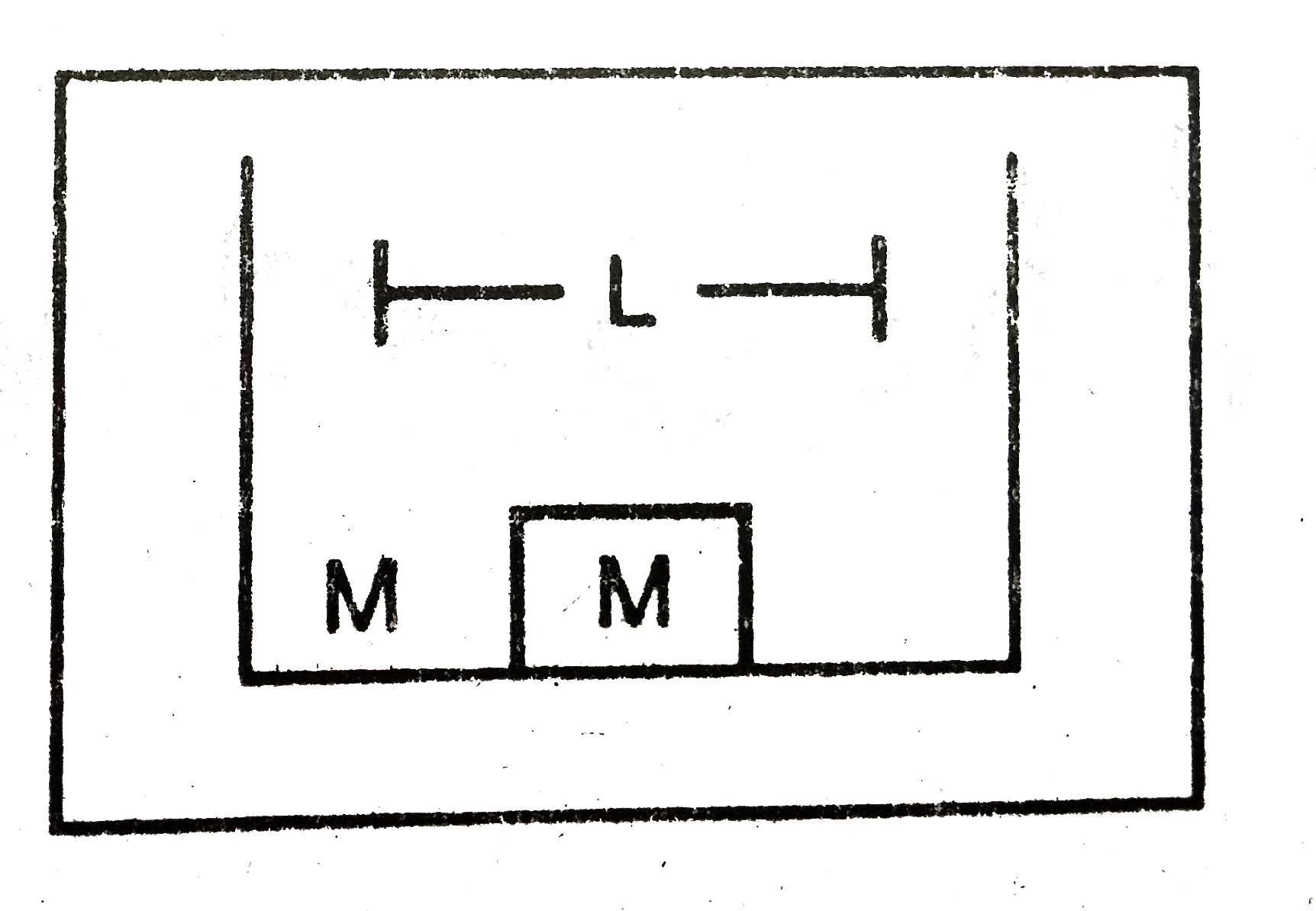
View SolutionConsider a gravity free hall in which a tray of mas M, carrying a cubical block of ice of mass m and edge L, is at rest in the middle.. If the ice melts, by what distance does the centre of mass of the tray plus the ice system descend?
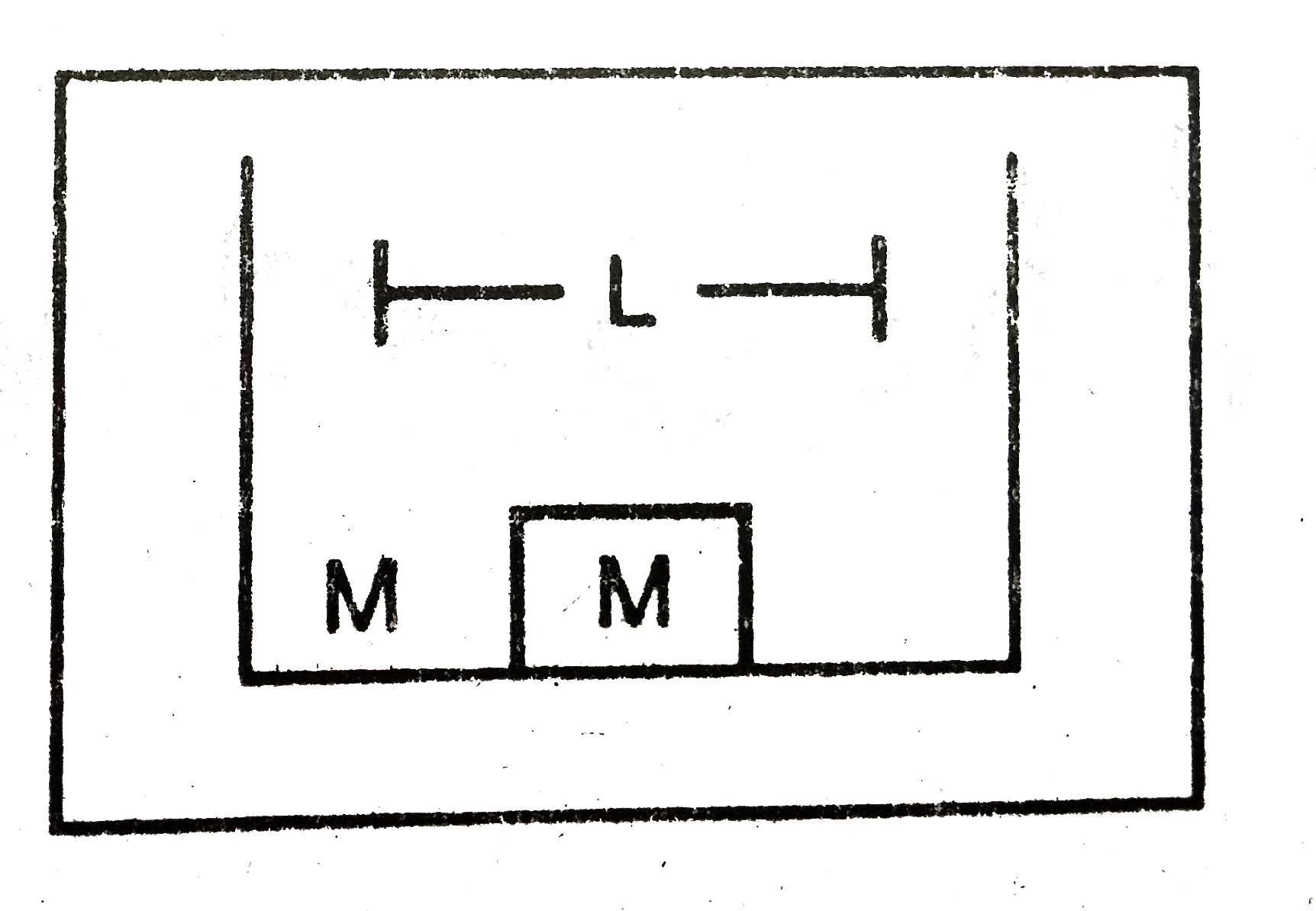
View SolutionA cubical ice block of side length 'a' is floating in water in a beaker. Find the change in height of the centre of mass of (water+ice) system when the ice block melts completely. It is given that ratio of mass of water to mass of ice originally in the containe is 4:1.
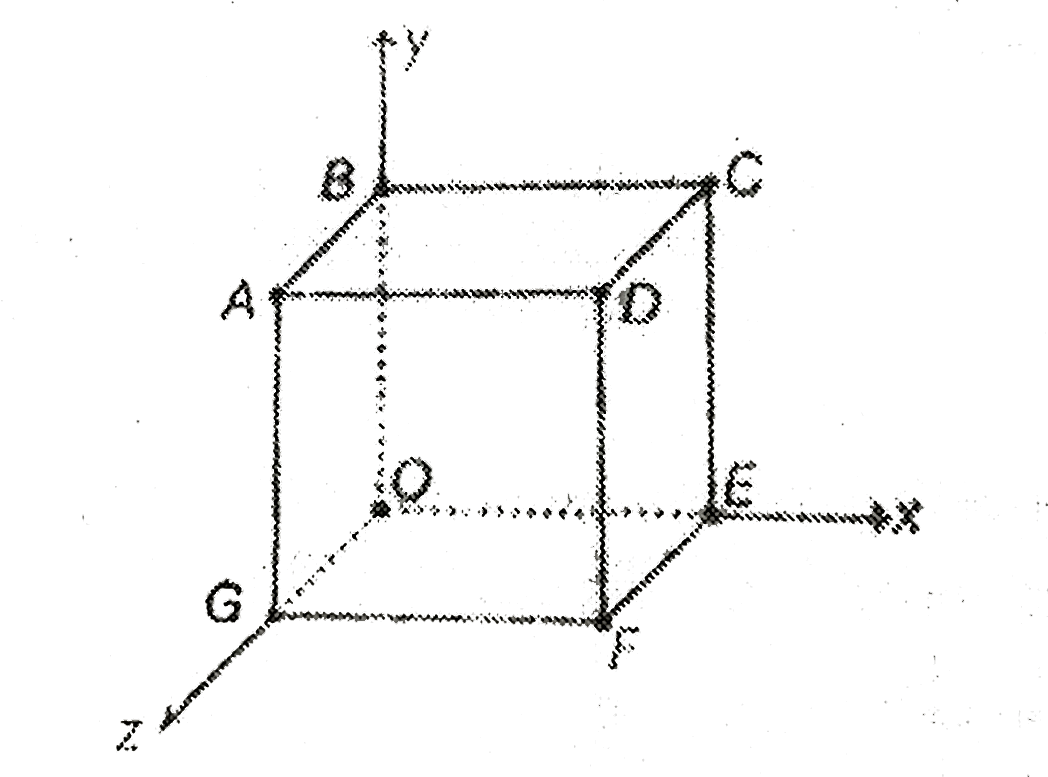
View SolutionSeven particles are placed at the seven corners of a cube of side 'a' (except at origin ) . The mass of each particle is 'm' . The centre of mass of the system is
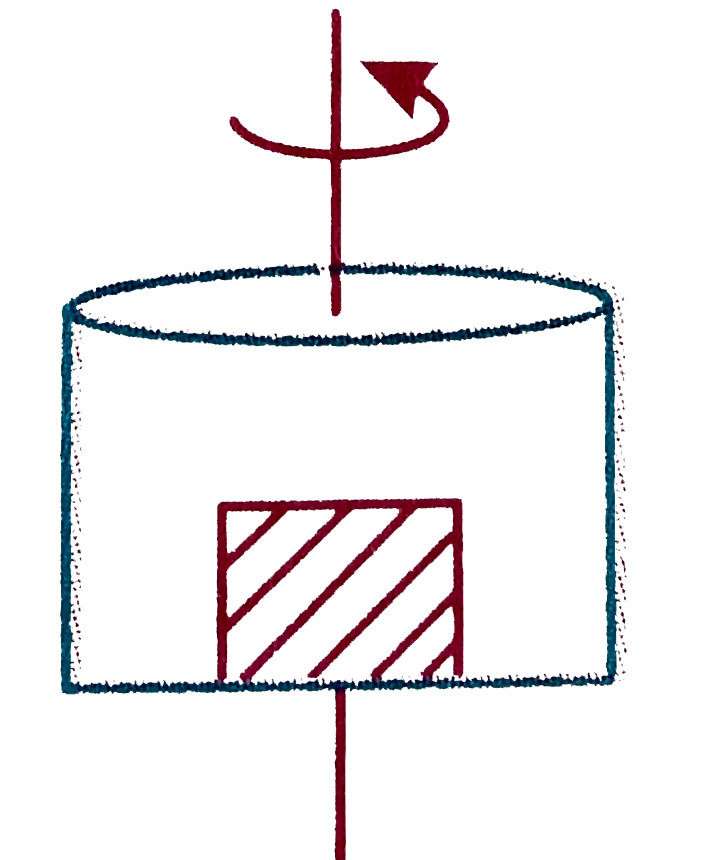
View SolutionAn ice block is in a trough which is rotating about vertical axis passing through its centre. When ice melts completely, the angular velocity of the system
View Solution
