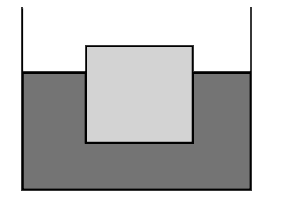
A cubical block of ice of mass m and edge L is placed in a large tray of mass M. If the ice melts, how far does the centre of mass of the system ''ice plus tray'' come down?

Video Solution

Text Solution

Verified by Experts

Consier ure. Suppose the centre of massof the tray is a distace $x_{1}$ above the origin and that of the ice is a distance $x_{2}$ above the origin. The height of the centre of mass of the ice tray system is
$x = \frac{m x_{2} + m x_{1}}{m + M}$

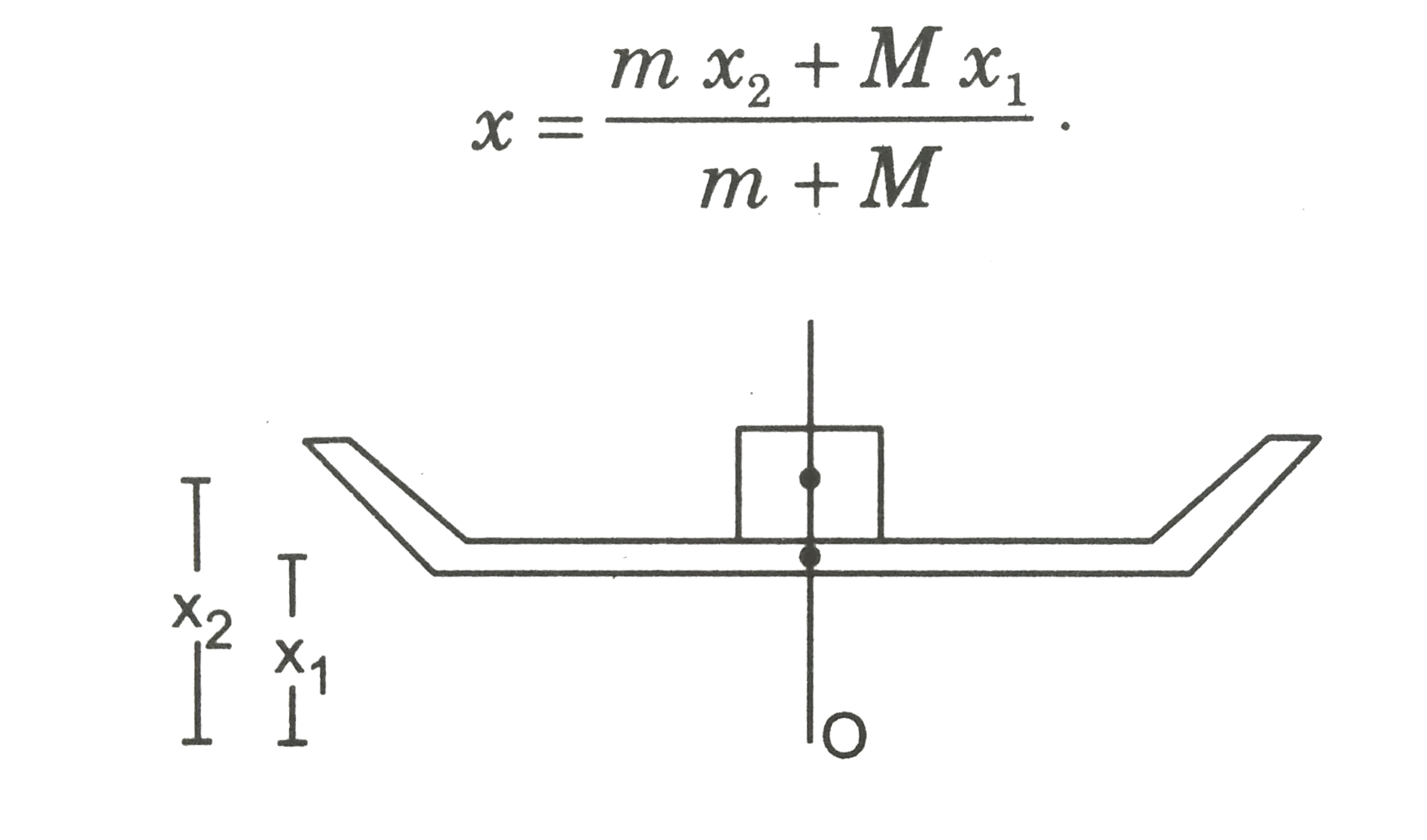
When the ice melts, the water of mass m spreads on the surface of the tray. As the tray is large, the height of water is then on the surfave of the tray and is at a distance $x_{2} - \frac{L}{2}$ above the origin. THe new centre of masss of theh ice -tray system will be at the height
$x' = \frac{m (x_{2} - \frac{L}{2}) + M x_{1}}{m + M}$
THe shift in the centre of mass $= x - x' = \frac{m L}{2 (m + M)}$

Updated on:21/07/2023

Two point masses m and M are separated by a distance L . The distance of the centre of mass of the system from m is
A $L (m / M)$
B $L (M / m)$
C $L (\frac{M}{m + M})$
D $L (\frac{m}{m + M})$
Two point masses m and M are separated bya distance L . The distance of the centre of mass of the system from m is
A $L (m / M)$
B $L (M / m)$
C $L (\frac{M}{m + M})$
D $L (\frac{m}{m + M})$