Find the acceleration of center of mass of the blocks of masses m1 and m2 (m1>m2) in Atwood.s machine:
We know from Newton.s laws of motion magnitude of acceleration of each block is
a=(m1−m2m1+m2)g
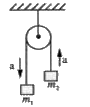
Now acceleration of their C.M is
acm=m1a+m2(−a)m1+m2,acm=(m1−m2m1+m2)a
acm=(m1−m2m1+m2)(m1−m2m1+m2)g
∴ Accleration of centre of mass acm=(m1−m2m1+m2)2g
Similar Questions
Find the acceleration of centre of mass of the blocks of masses m1,m2(m1>m2) in Atwood's machine.
View SolutionThree blocks, placed on smooth horizontal surface are connected by ideal string and a disc shaped pulley of radius r, and mass m. Find the accelerations of the blocks. Masses of the blocks are given as M1=10kg,M2=5kg,M3=2kg,m=2kg.
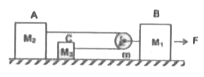
View Solution
Knowledge Check
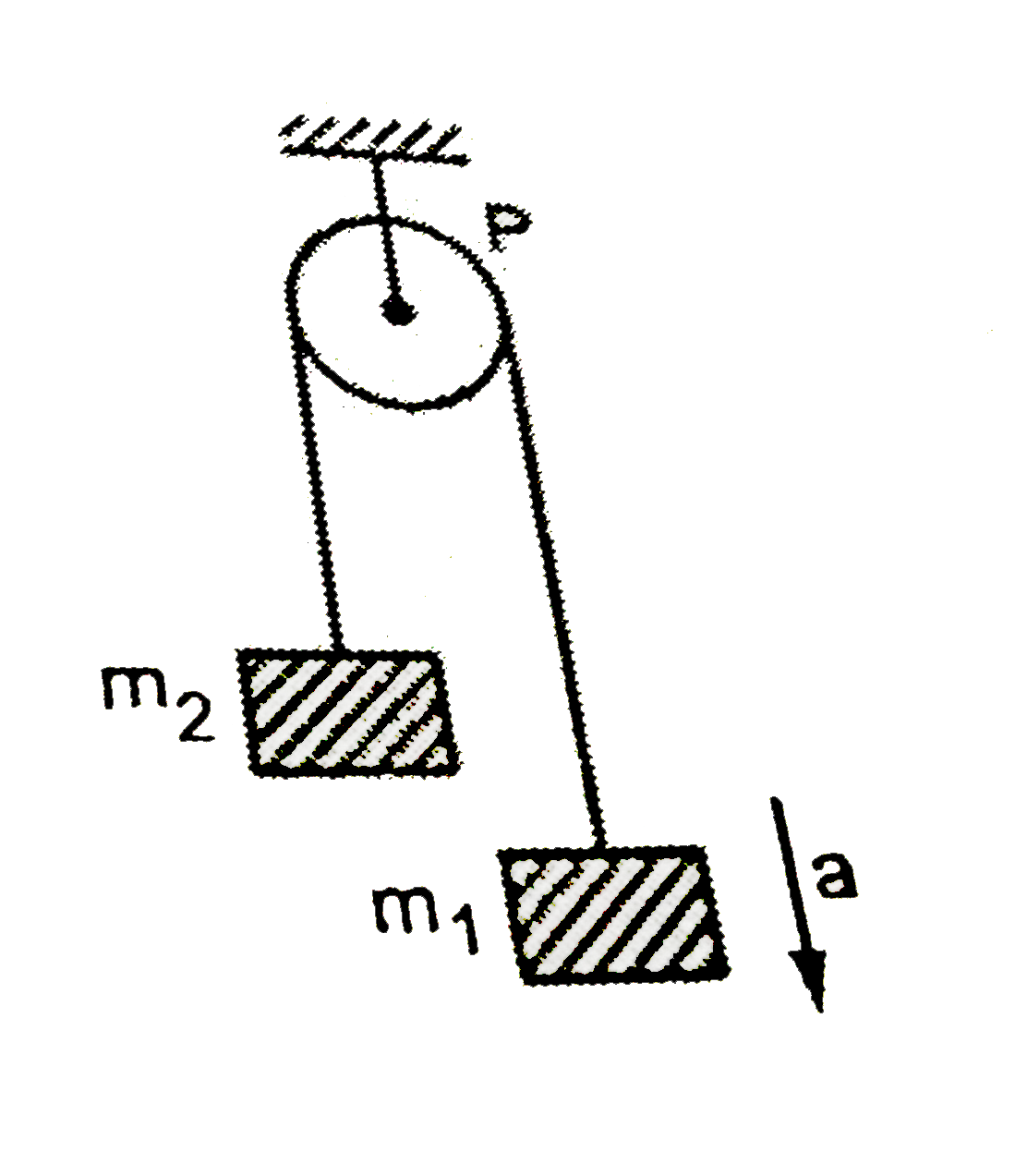
In the figure, the blocks have unequal masses m1 and m2(m1>m2).m1 has a downward acceleration a . The pulley P has a radius r, and some mass. The string does not slip on the pulley.AThe two sections of the string have unequal tensions.BThe two blocks have acceleration of equal magnitude.CThe angular acceleration of P is a/r.Da<(m1−m2m1+m2)
Find the acceleration of each block in the figure shown below, in terms of their masses m1,m2 and g. Neglect any friction.
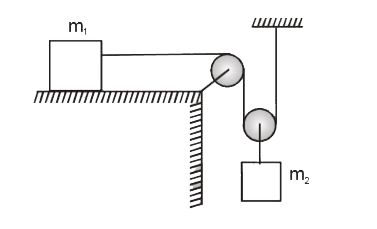
View Solution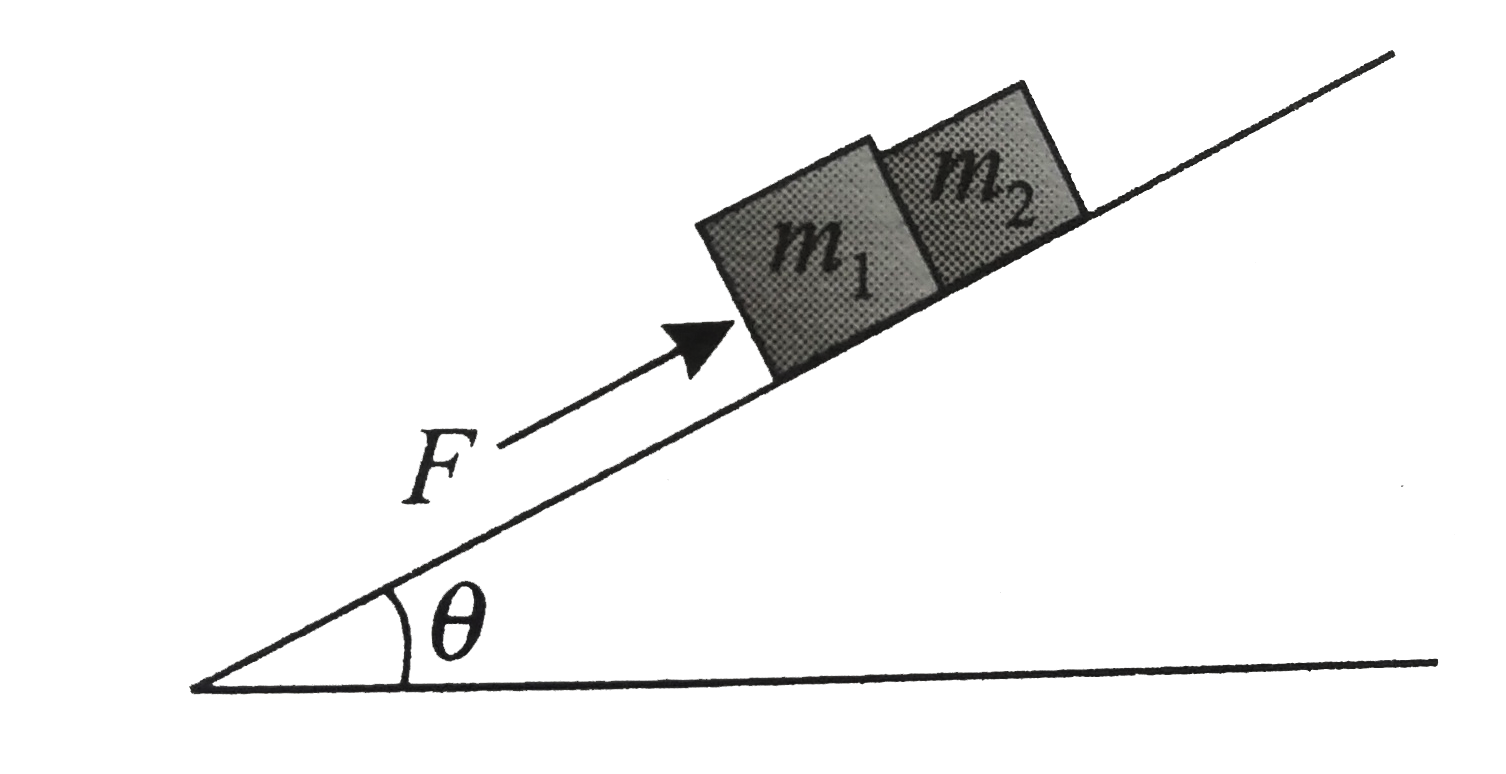
Two blocks are placed at rest on a smooth fixed inclined place. A force F acts on block of mass m1 and is parallel to the inclined plane as shown in figure. Both blocks move up the incline. Then
(i) Draw free body diagram blocks of mass m1 and blocks mass m2
(ii) Find acceleration of blocks of mass m1 and blocks mass m2
(iii) Find normal reaction between the blocks of mass m1 and m2
View Solution
Two blocks are placed at rest on a smooth fixed inclined place. A force F acts on block of mass m1 and is parallel to the inclined plane as shown in figure. Both blocks move up the incline. Then
(i) Draw free body diagram blocks of mass m1 and blocks mass m2
(ii) Find acceleration of blocks of mass m1 and blocks mass m2
(iii) Find normal reaction between the blocks of mass m1 and m2
View SolutionFigure shows a block of mass m1 sliding on a block of mass m2, with m1>m2. Find the

(a) acceleration of each block
(b) tension in the string
(c ) force exerted by m1 on m2. ltbr> (d) force exerted by m2 on the incline.
View SolutionFigure shows a block of mass m1 sliding on a block of mass m2, with m1>m2. Find the

(a) acceleration of each block
(b) tension in the string
(c ) force exerted by m1 on m2. ltbr> (d) force exerted by m2 on the incline.
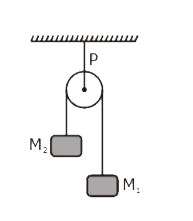
View SolutionIn the figure, the blocks have masses M1andM2(M1>M2) and acceleration a. The pulley P has a radius r and some mass the string not slip on the pulley
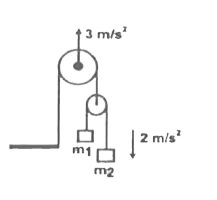
View SolutionIn the figure shown, the acceleration of block of mass m2 is 2m/s2. The acceleration of m1 :
View Solution
