In the figure, the blocks have masses M1andM2(M1>M2) and acceleration a. The pulley P has a radius r and some mass the string not slip on the pulley
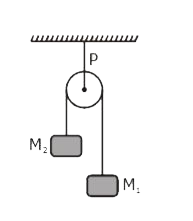
The two sections of the string have unequal tensions
The two blocks have acceleration of unequal magnitude
The angular acceleration of P is ar
angular acceleration of the pulley is zero.
The correct Answer is:A,C
Step by step video & image solution for In the figure, the blocks have masses M_(1) and M_(2) (M_(1) gt M_(2)) and acceleration a. The pulley P has a radius r and some mass the string not slip on the pulley by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- 10 ROTATIONALBOOK - MOTIONCHAPTER - 10 ROTATIONALEXERCISE - Exercise - 2 (Level -I)
51 Videos
- 10 ROTATIONALBOOK - MOTIONCHAPTER - 10 ROTATIONALEXERCISE - Exercise - 2 (Level - II)
25 Videos
- 10 ROTATIONALBOOK - MOTIONCHAPTER - 10 ROTATIONALEXERCISE - Example 31
1 Videos
- ALTERNATING CURRENTBOOK - MOTIONCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - 4 (LEVEL - II)
14 Videos
Similar Questions
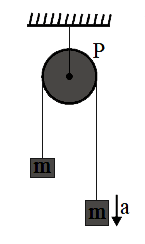
In the figure, the blocks unequal masses m1 and m2 (m1<m2).m2 has a downward acceleration a. The pulley P has a radius r, and some mass. The string does not slip on the pulley. Find the acceleration of block and angular acceleration of pulley. (I = momentum of inerita of pulley)
View SolutionTwo blocks are connected by a string that passes over a pulley of radius R and moment of inertia I. The block of mass m1 sides on a frictionless, horizontal surface, the block of mass m2 is suspended from the string. Find the acceleration a of the blocks and the tension T1 and T2 assuming that the string does not slip on the pulley.

View Solution
Knowledge Check
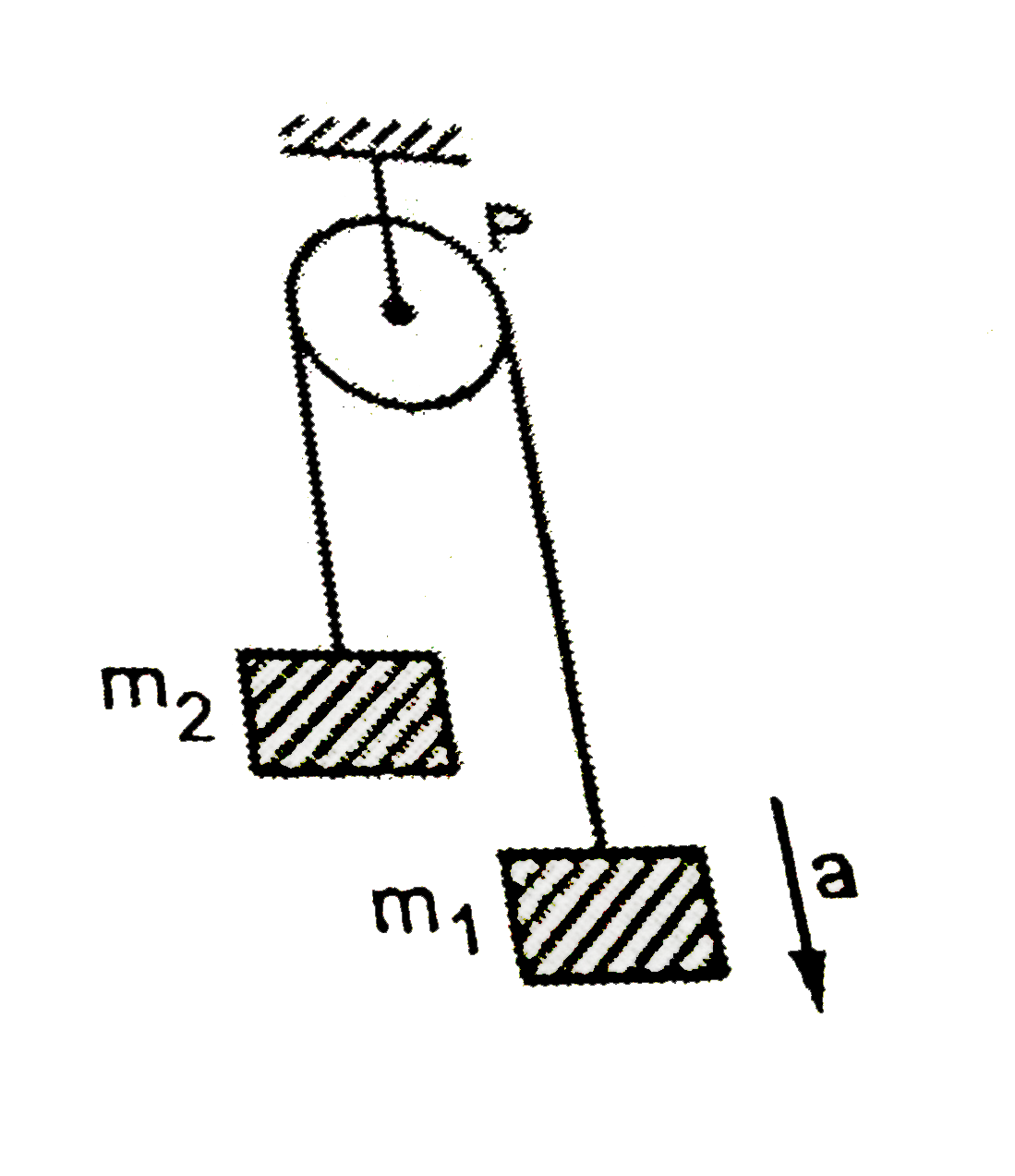
In the figure, the blocks have unequal masses m1 and m2(m1>m2).m1 has a downward acceleration a . The pulley P has a radius r, and some mass. The string does not slip on the pulley.AThe two sections of the string have unequal tensions.BThe two blocks have acceleration of equal magnitude.CThe angular acceleration of P is a/r.Da<(m1−m2m1+m2)On a pulley of mass M hangs a rope with two masses m1 and m2(m1>m2) tied at the ends as shown in the figure. The pulley rotates without any friction, whereas the friction between the rope and the pulley is large enough to prevent any slipping. Which of the following plots best represents the difference between the tensions in the rope on the two sides of the pulley as a function of the mass of the pulley ?
 A
A B
B C
C D
D
A block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
Amg2m+MB2mgm+MCmgm+MD2mg2m+M
Two masses m1 and m2(m2>m1) are hanging vertically over frictionless pulley. The acceleration of the two masses is :

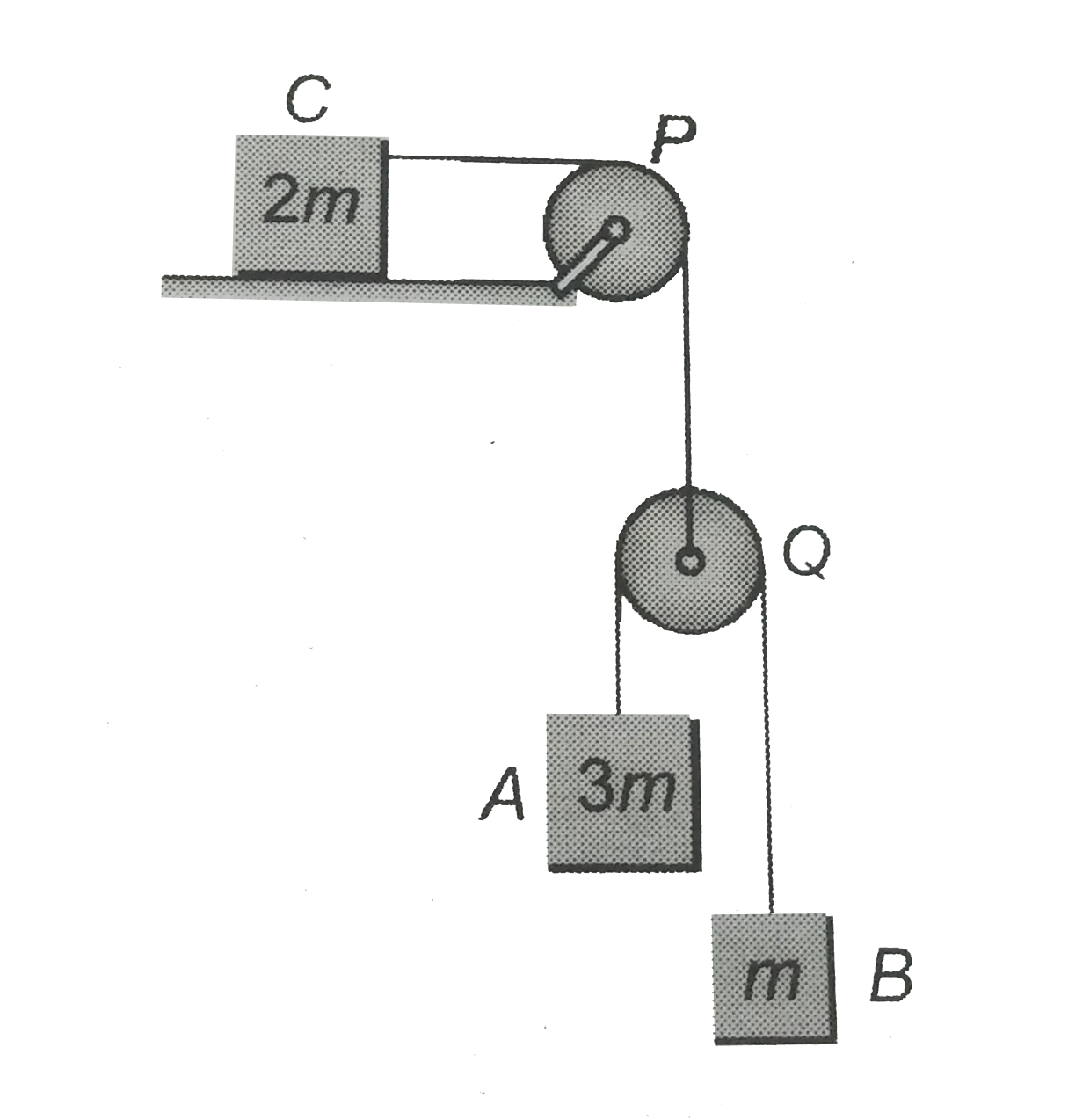
View SolutionIn the arrangement shown in the figure, the blocks have masses 3m,m and 2m, the friction is absent, the masses of the pulleys and the threads are negligible. Find the acceleration of mass 3m.
View SolutionFigure shows two blocks of mass m and m connected by a string passing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley (uniform disc) has mass m and it can freely rotate about this axis. Find the acceleration of the mass m assuming that the string does not slip on the pulley.
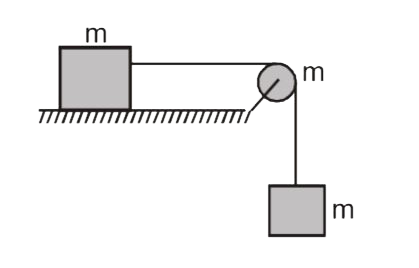
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo masses m1 and m2 are joined with the help of massless string passing over a pulley of Radius R and mass M. Assume that string doesn't slip over the pulley. Take m1=10kg, m2=5kg, M=10kg, R=1m.

(a) Calculate the acceleration of each book.
(b) Calculate the tensions in the thread.
View Solution
