A uniform solid sphere is rolled up a fixed rough inclined surface with an initial speed of u. Assuming that there is no slip find the maximum height reached by the sphere over the incline. Solution in Telugu
When there is no slip between the incline and the sphere, mechanical energy can be conserved.
Initial kinetic energy of the sphere
=12mu2+12Icmω2=12mu2(1+25)=710mu2
Final gravitatonal potential energy with respect to the initial position is mgh.
Therefore, maximum height reached is 7u210g.
Similar Questions
Two uniform solid spheres having unequal radii are released from rest from the same height on a rough incline. If the spheres roll without slipping
View SolutionA uniform solid sphere is rolled up a fixed rough inclined surface with an initial speed of u. Assuming that there is no slip find the maximum height reached by the sphere over the incline.
View SolutionA solid spherical ball is rolling without slipping towards a fixed inclined plane with speed V0. Find the maximum height, that the ball reached on the incline.
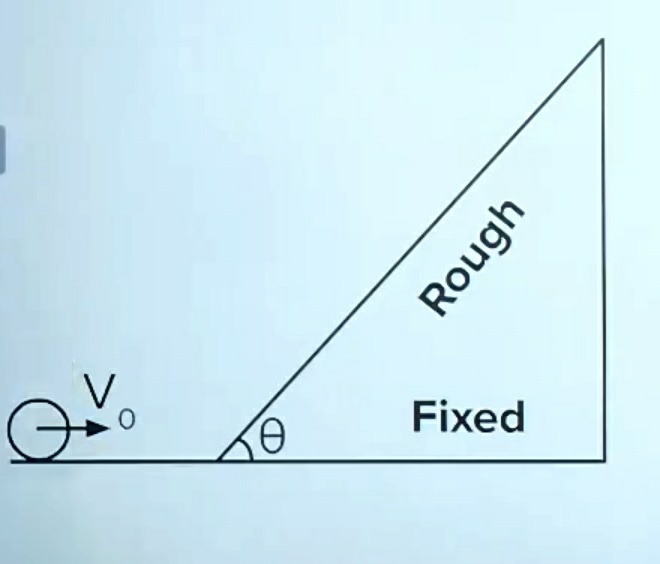
View SolutionA uniform solid sphere is rolled up a fixed rough inclined surface with an initial speed of u. Assuming that there is no slip find the maximum height reached by the sphere over the incline.
View SolutionTwo uniform solid spheres having unequal radii are released from rest from the same height on a rough incline. the spheres roll without slipping
View SolutionA uniform solid sphere rolls on a horizontal surface with a linear speed of 10 m/s. It then rolls up a.plane inclined at 30° to horizontal. What is the height upto wlrich the sphere rises ? (See Fig.) Assume that the surface is frictionless. Also calculate the distance travelled by the Fig. sphere on the inclined plane ?
View SolutionA uniform solid sphere rolls up (witout slipping) the fixed inclined plane, and then back down. Which is the correct graph of acceleration a of centre of mass of solid sphere as function of time t (for the duration sphere is on the incline)? Assume that the sphere rolling up has a positive velocity.
View Solution
