Question

A uniform solid sphere rolls on a horizontal surface with a linear speed of 10 m/s. It then rolls up a.plane inclined at 30° to horizontal. What is the height upto wlrich the sphere rises ? (See Fig.) Assume that the surface is frictionless. Also calculate the distance travelled by the Fig. sphere on the inclined plane ?

Explanation

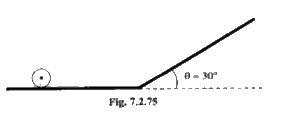
`mgh = (1//2)mv^(2) = (1//2) (2//3)mr^(2) xx (v^(2)//r^(2)) =(7//10)mr^(2), h=7v^(2)//10g = 7 xx 10^(2)//10 g = 7.14 m,s = 14.3`m