H2 gas undergoes process where pV2 = constant. The ratio of work done by gas to modulus of change in its internal energy as the gas expands is 2/N. N is is equal to
The correct Answer is:5
Topper's Solved these Questions
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - LECTURE SHEET (EXERCISE - IV (STRAIGHT OBJECTIVE TYPE QUESTIONS))
3 Videos
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - LECTURE SHEET (EXERCISE - IV (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS))
1 Videos
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - LECTURE SHEET (EXERCISE - III (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS))
3 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) PRACTICE SHEET (ADVANCED) Integer/Subjective Type Questions
2 Videos
- THERMOMETRY BOOK - AAKASH SERIESCHAPTER - THERMOMETRY EXERCISE - Numerical Exercise (LEVEL- 1)
11 Videos
Similar Questions
[H_(2)" gas undergoes process where "PV^(2)=" constant.The ratio of work done by gas to modulus of change in "],[" its internal energy as the gas expands is "(2)/(N).N" is equal to "]
View SolutionAn ideal monoatomic gas undergoes a process in which its internal energy U and density ρ vary as Uρ= constant. The ratio of change in internal energy and the work done by the gas is
View Solution
Knowledge Check
In an adiabatic process 90 J of work is done on the gas. The change in internal energy of the gas is
A−90jB+90jC0 jDDepends on initial temperatureA monoatomic gas follow a process TV= constant. Calculate the ratio of work done to change in internal energy when the gas goes form one state to another.
A23B−23C53D75An ideal monoatomic gas undergoes a process in which its internal energy U and density ρ vary as Uρ= constant. The ratio of change in internal energy and the work done by the gas is
A(a) 32B(b) 23C(c) 13D(d) 35
An ideal monoatomic gas undergoes a process in which its internal energy U and density ρ vary as Uρ= constant. The ratio of change in internal energy and the work done by the gas is
View SolutionA certain amount of mono - atomic ideal gas undergoes a process ρUn= constant where ρ is density of gas and U is internal energy of the gas.It is found that the ratio WδU for this process is 23. Find the value of n.
View SolutionAn ideal gas undergoes cyclic process ACBC as shown is given PV diagram
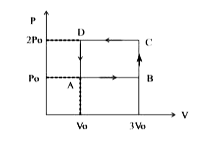
The amount of work done by the gas is
View SolutionIn an adiabatic expansion of 2 moles of a gas, the change in its internal energy was found to be –100J. The work done in this process is :
View SolutionAn ideal gas with adiabatic exponent (γ=1.5) undergoes a process in which work done by the gas is same as increase in internal energy of the gas. Here R is gas constant. The molar heat capacity C of gas for the process is:
View Solution
