(i) For the wave on a string described in Exercise 15.11. do all the points on the string oscillate with the same (a) frequency , (b) phase , (c ) amplitude? Explain your answers. (ii) What is the amplitude of a point 0.375 m away from one end?
(a) All the points except the nodes on the string have the same frequency and phase, but not the same amplitude. (b) 0.042m
Similar Questions
(i) For the wave on a string described in question, do all theh points on the string oscillate with the same (a) frequency, (b) phase, (c) amplitude ? Explain your answers. (ii) What is the amplitude of a point 0.375m away from one end?
View Solution(i) The transverse displacement of a string (clamped at its two ends ) is given by y(x,t)=0.06sin[2π3x]cos120πt,
where x, y are in m and t is in s.
Do all the points on the string oscillate with the same (a) frequency, (b) phase, (c) amplitude ? Explain your answers.
View Solution
Knowledge Check
The displacement of a vibrating string versus position along the string is shown in the figure. The periodic wave have a speed of 10.0cm/s. A and B are two points on the string.
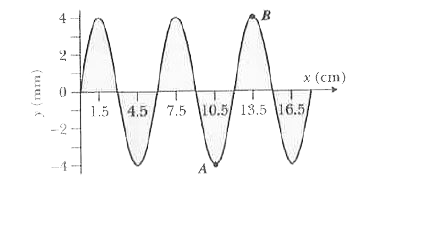
What is the amplitude of the wave?A2 mmB4 mmC12 mmD8 mm
The transverse displacement of a string (clamped at its two ends ) is given by y(x,t)=0.06sin(2π)3xcos120πt,
where x, y are in m and t is in s.
Do all the points on the string oscillate with theh same
(a) frequency (b) phase (c) amplitude
Explain your answer.
View SolutionAdjacent antinodes of a standing wave on a string are 15.0 cm apart. A particle at an antinode oscillates in simple harmonic motion with amplitude 0.850 cm and period 0.0750 s. The string lies along the +x-axis and is fixed at x=0.
(a) find the displacement of a point on the string as a function of position and time.
(b) Find the speed of propagation of a transverse wave in the string.
(c) Find the amplitude at a point 3.0 cm to the right of an antinode.
View SolutionAdjacent antinodes of a standing wave on a string are 15.0 cm apart. A particle at an antinode oscillates in simple harmonic motion with amplitude 0.850 cm and period 0.0750 s. The string lies along the +x-axis and is fixed at x=0.
(a) find the displacement of a point on the string as a function of position and time.
(b) Find the speed of propagation of a transverse wave in the string.
(c) Find the amplitude at a point 3.0 cm to the right of an antinode.
View SolutionA transverse harmonic wave is propagating along a taut string. Tension in the string is 50 N and its linear mass density is 0.02kgm–1 The string is driven by a 80Hz oscillator tied to one end oscillating with an amplitude of 1mm. The other end of the string is terminated so that all the wave energy is absorbed and there is no reflection
(a) Calculate the power of the oscillator.
(b) The tension in the string is quadrupled. What is new amplitude of the wave if the power of the oscillator remains same?
(c) Calculate the average energy of the wave on a 1.0m long segment of the string.
View SolutionAn harmonic wave has been set up on a very long string which travels along the length of the string. The wave has a frequency of 50 Hz, amplitude 1 cm and wavelength 0.5 m. find
(a) the time taken by the wave to travel a distance of 8 m along the length of string (b) the time taken by a point on the string to travel a distance of 8 m, once the wave has reached the point and sets it into motion (c ) also. consider the above case when the amplitude gets doubled
View SolutionAn harmonic wave has been set up on a very long string which travels along the length of the string. The wave has a frequency of 50 Hz, amplitude 1 cm and wavelength 0.5 m. find
(a) the time taken by the wave to travel a distance of 8 m along the length of string (b) the time taken by a point on the string to travel a distance of 8 m, once the wave has reached the point and sets it into motion (c ) also. consider the above case when the amplitude gets doubled
View SolutionA 660 Hz tuning fork sets up vibration in a string clamped at both ends. The wave speed for a transverse wave on this string is 1220ms−1 and the string vibrates in three loops. (a) Find the length of the string. (b) If the maximum amplitude of a particle is 0.5 cm, write a suitable equation describing the motion.
View Solution
