A 660 Hz tuning fork sets up vibration in a string clamped at both ends. The wave speed for a transverse wave on this string is 1220ms−1 and the string vibrates in three loops. (a) Find the length of the string. (b) If the maximum amplitude of a particle is 0.5 cm, write a suitable equation describing the motion.
The correct Answer is:a) 50cm
b) cos(0.06πcm−1)sin((1320πs−1)t)
Frequency of the tunning fork,
f=660Hz
Wave speed v=220ms
→lamda=Vf=220660=13m
No.of loops = 3
a. So, L.f=(32)v
→L.660=(32)×220
L=12m=50cm
b. the equation of resultant statioN/Ary wave is given by,
y=2Acos(2πxλ)sin(2πvtλ)
→y=(0.5)cos⎛⎝2πx13m⎞⎠sin(2π×220×tλ)
→y=(0.5cm)
cos(6πxm−1)sin(1320πs−1t)
→y=(0.5cm)
cos(0.06πcm−1)sin(1320πs−1t)
Topper's Solved these Questions
Similar Questions
The vibrations from an 800 Hz tuning fork set up standing waves in a string clamped at both ends. The wave speed in the string is known to be 400m/s for the tension used. The standing wave is observed to have four antinodes. How long is the string?
View SolutionA string of 2 m length is fixed at both the ends . The transverse wave created in it propogates with a speed of 50ms−1 . If the string is made to vibrate with three loops , find the frequency of the wave produced .
View Solution
Knowledge Check
If the speed of a transverse wave on a stretched string of length 1 m is 60ms−1, what is the fundamental frequency of vibration ?
A40 HzB45 HzC35 HzD30 HzThe fundamental frequency of a stretched string fixed at both the ends is 50 Hz. If the velocity fo transverse wave created in string is 10ms−1 , find its length .
A0.1 mB0.0001 mC100 mD1000 mA stretched string is fixed at both its ends. Three possible wavelengths of stationary wave patterns that can be set up in the string are 90 cm, 60 cm and 45 cm. the length of the string may be
A80 cmB120 cmC90 cmD45 cm
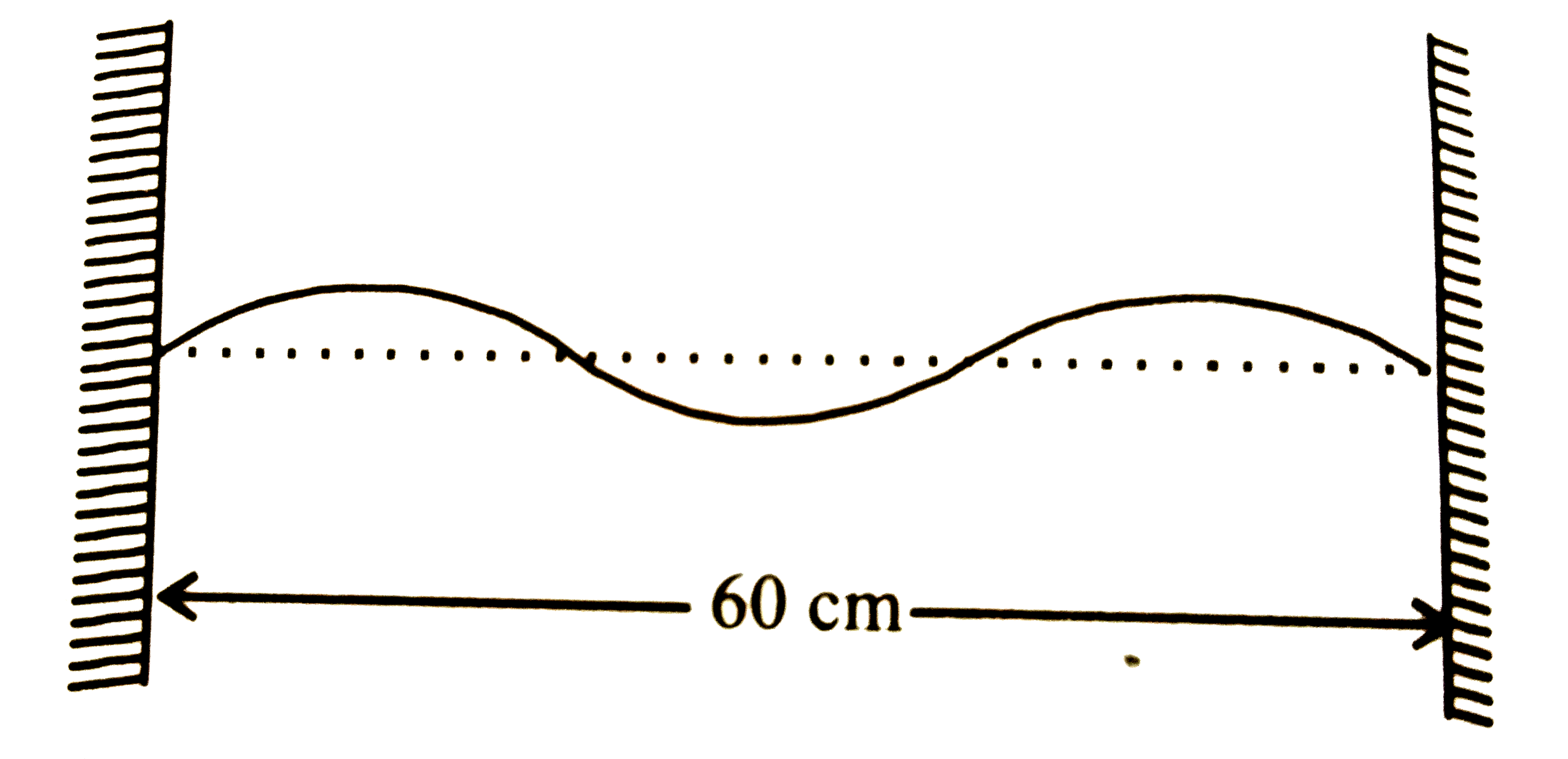
The standing wave pattern along a string of length 60 cm is shown in the above diagram. If the speed of the transverse waves on this string is 300 m/s, in which one of the following modes is the string vibrating?
View SolutionA string of mass per unit length μ is clamped at both ends such that one end of the string is at x = 0 and the other is at x=l. When string vibrates in fundamental mode, amplitude of the midpoint O of the string is a, tension in a, tension in the string is T and amplitude of vibration is A. Find the total oscillation energy stored in the string.
View SolutionThe length, mass and tension of a string are 1000 cm, 0.01 Kg and 10 N respectively. The speed of transverse waves in the string will be -
View SolutionA string 1m long is drawn by a 300 Hz vibrator attached to its end. The string vibrates in three segments. The speed of transverse waves in the string is equal to
View SolutionA person vibrates the end of a string sending transverse waves down the string. If the person then doubles the frequency at which he vibrates the string, the speed of the waves
View Solution
