Two isolated uniform spheres of masses $m_{1}$ and $m_{2}$ and radii 2R and R respectively are released from rest from the given position. Find the distance from $m_{1}$ where they meet.

(Position of centre of mass does not change as gravitational force acting between them is an internal force)

Text Solution

Verified by Experts

$(\frac{m_{2}}{m_{1} + m_{2}}) 3 R$

Updated on:21/07/2023

Two homogeneous spheres A and B of masses m and 2m having radii 2a and a respectively are placed in touch . The distance of the centre of mass from the first sphere is
Aa
B $2 a$
C $3 a$
Dnone of these
Two spherical bodies of masses $m$ and $4 m$ and radii R and 2R respectively are released in free space with initial separation between their centres equal to 15 R. If they attract each other due to gravitational force only, then the distance covered by smaller sphere just before collision will be

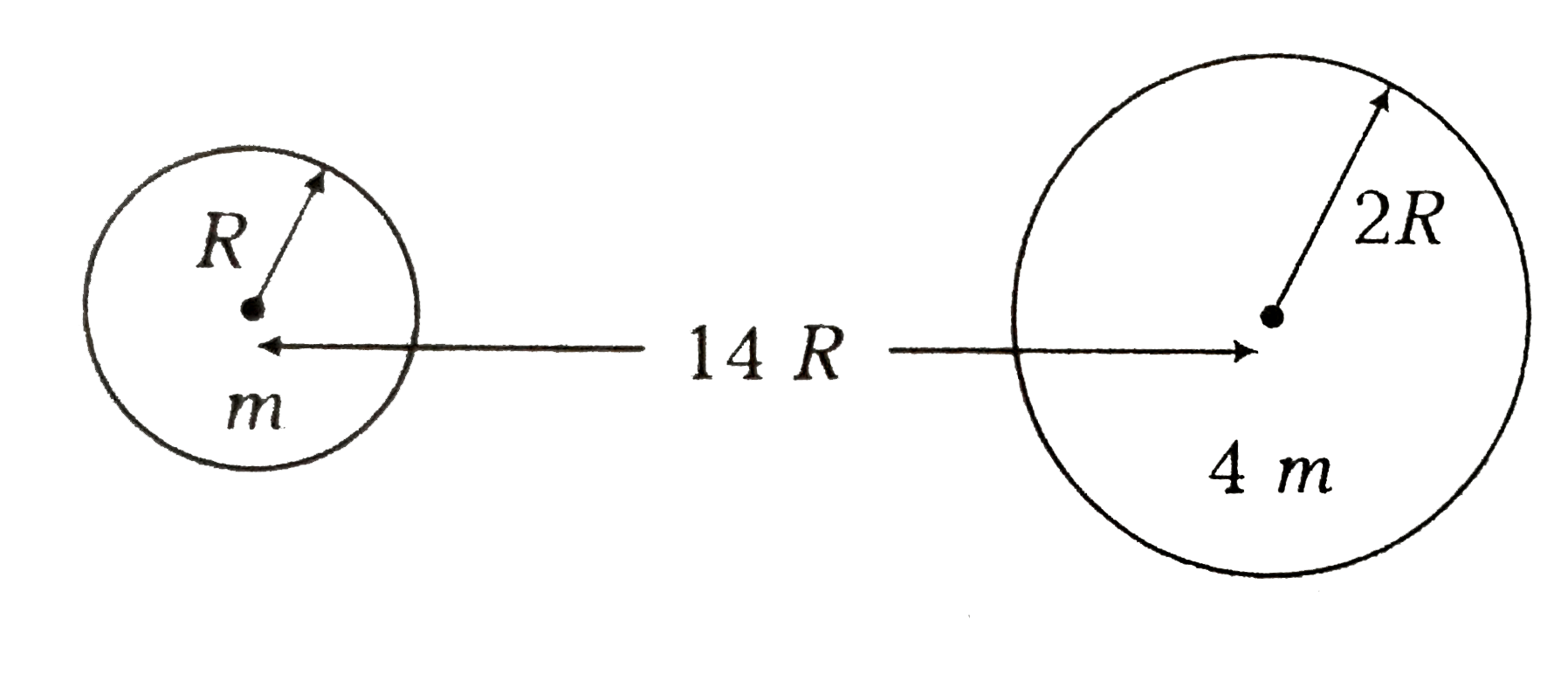A5 R
B9.6 R
C2.5 R
D6 R
Two spherical bodies of masses m and 6m and radii R and 2R respectively are released in free space with initial separation between their centres equal to 10 R . If they attract each other due to gravitational force only , then the distance covered by smaller sphere just before collisions will be
A6 R
B7.5 R
C2.5 R
D9 R