A ball is projected with an initial velocity .u. at an angle .θ. to the horizontal surface ad shown in figure. If .e. is the coefficient of restitution between the ball and the surface, then

(a) Time it takes for 1st collision is T = 2usinθg
(b) The time interval between 1stand2nd collisions is T1=2(eu)sinθg=eT
(c ) Similary, the time interval between 2ndand3rd collisions is T2=2(e2u)sinθg=e2T
(d) The total time taken by the ball to settle on the surface is
T0=T+T1+T2+......=T+eT+e2T....
=T[1+e+e2+....]∴T0=T(1−e)
(e ) If the collision is elastic, then e = 1 and T0=∝
(ii) (a) The horizonta distance covered by the ball before 1st collision is
R=u2sin2θg=ucosθ×T
(b) The horizontal distance covered by it between 1st and 2nd collisions is R1=ucosθ×eT=eR
(c ) Similarly, the horizontal distance covered between 2ndand3rd collisions is
R2=ucosθ×e2T=e2R
(d) Total horizontal distance (or) range covered by the ball before it settles on the ground is
R0=R+Rl+R2+....R+eR+e2R+....
R[1+e+e2+...]∴R0=R(−e)
(c ) If the collision is elastic, then e = 1 and R0=∝
(iii) (a) The maximum height reached by the ball before 1st collision is
H=u2sin2θ2g=(usinθ)22g
(b) Maximum height it reaches between 1stand2nd collisions is H1(eusinθ)22g=e2H
(c ) Similarly maximum height between 2ndand3rd collisions is H2=(e2usintheta)22g=e4H
(d) The sum of the maximum heights reached by the ball before it settles on the surface is
H0=H+H1+H2+......H+e2H+e4H+.....
=H+e2H[1+e2+......]+H+e2H[11−e2]∴H0=H1−e2
(e) If the collision is elastic, then e = 1 and H0=∝
Topper's Solved these Questions
- WORK, POWER & ENERGY BOOK - AAKASH SERIESCHAPTER - WORK, POWER & ENERGY EXERCISE - EXERCISE - I
78 Videos
- WORK, POWER & ENERGY BOOK - AAKASH SERIESCHAPTER - WORK, POWER & ENERGY EXERCISE - EXERCISE - II (SCALARS (OR) DOT PRODUCT)
9 Videos
- WORK POWER ENERGYBOOK - AAKASH SERIESCHAPTER - WORK POWER ENERGYEXERCISE - EXERCISE - 3
61 Videos
Similar Questions
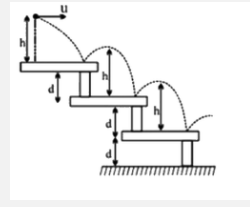
A ball is thrown horizontally from a height h above a staircase as shown in the figure. If the coefficient of restitution for any collision between the ball and the staircase is e, then the value of h for which the ball will bounce the same height above each step, is
View SolutionA ball moving with speed v collides with a horizontal smooth surface at an angle θ with normal to surface as shown in figure. If coefficient of restitution of collision is e, then find v'

View Solution
Knowledge Check
A ball of mass m is projected with a velocity 'u' at angle θ with the horizontal. It collides with a smooth box of mass 'M' at its highest position. If the co-efficient of restitution is 'e'.

Find the horizontal distance travelled by the ball before collision.Au22sinθcosθgBu2sinθcosθgCu2sinθcosθ2gDu2sinθcosθ4gA ball is projected with initial velocity u at an angle θ to the horizontal. Then horizontal displacement covered by ball as it collides third time to the ground would be, if coefficient of restitution is e :
 A(1+e)u2sin2θgBeu2sin2θgC(1−e)u2sin2θgD(1+e+e2)u2sin2θg
A(1+e)u2sin2θgBeu2sin2θgC(1−e)u2sin2θgD(1+e+e2)u2sin2θgA ball of mass m is projected with a velocity 'u' at angle θ with the horizontal. It collides with a smooth box of mass 'M' at its highest position. If the co-efficient of restitution is 'e'.
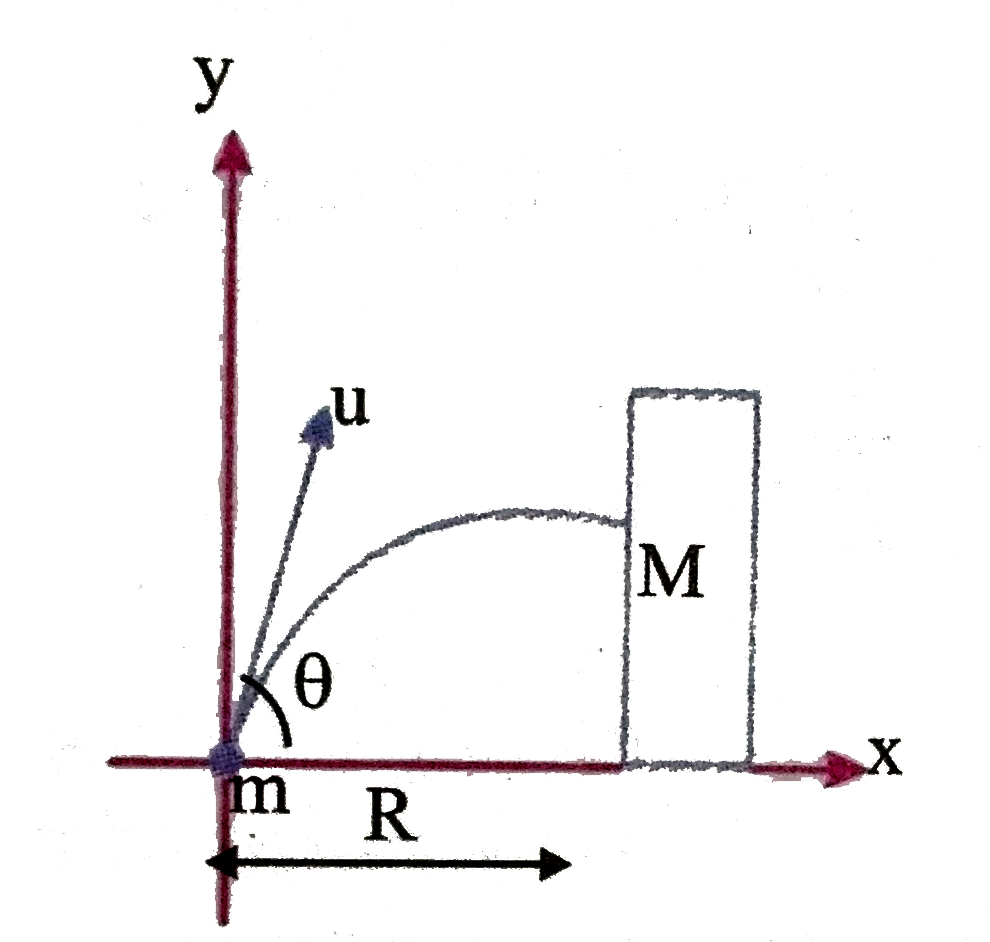
FInd the velocity of the ball after collisionA(m−eMM+m)ucosθB(M−emM+m)ucosθC(m+eMM+m)usinθD(m−eMM+m)usinθ
A ball moving with speed v collides with a horizontal smooth surface at an angle θ with normal to surface as shown in figure. If coefficient of restitution of collision is e, then find v'

View SolutionAn inelastic ball is projetced with a velocity 'u' at an angle 'α' to the horizontal, towards a wall distant 'd' from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is 'e')
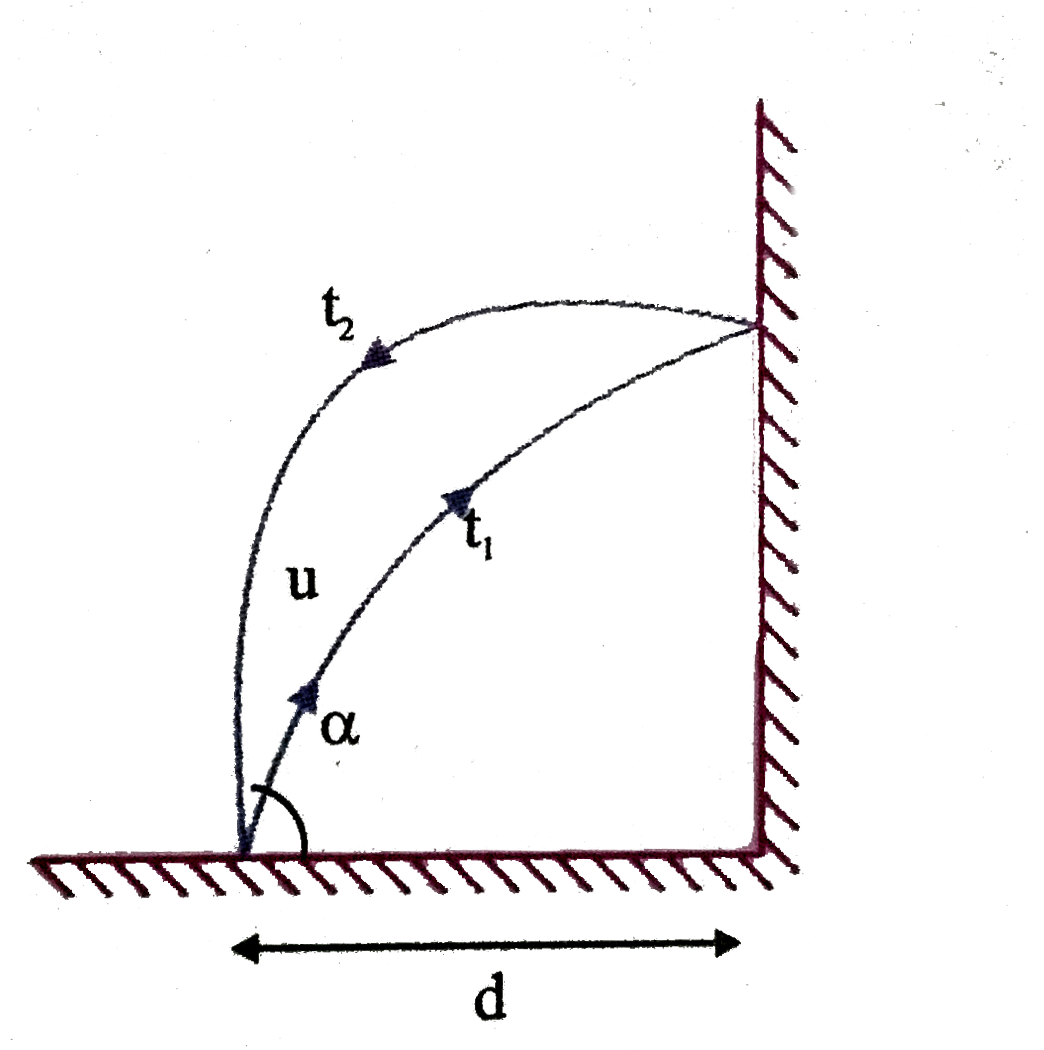
If the line joining the point of projection and the point of impact makes an angle 'θ' with the horizontal, then tanθ is
View SolutionAn inelastic ball is projetced with a velocity 'u' at an angle 'α' to the horizontal, towards a wall distant 'd' from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is 'e')
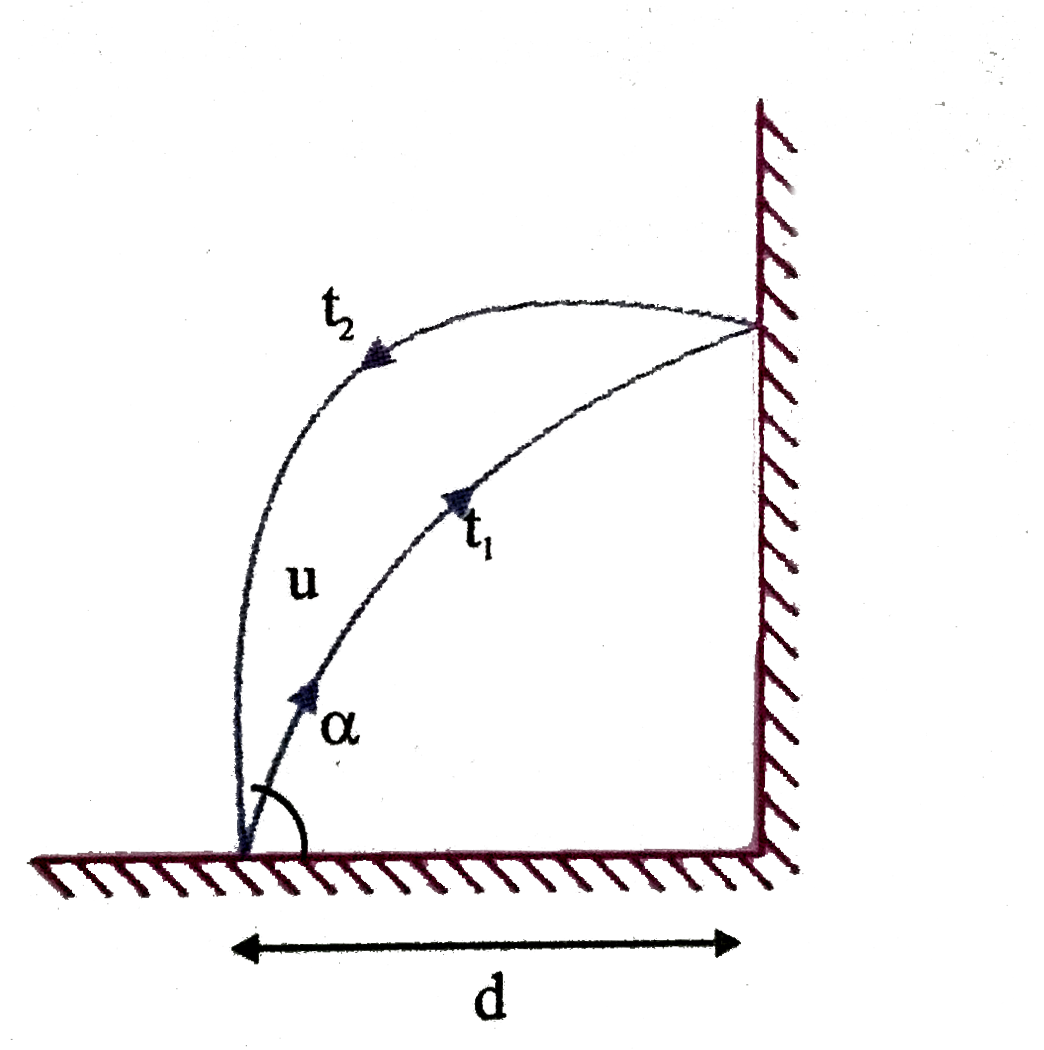
The total time of journey of the ball is
View SolutionAn inelastic ball is projetced with a velocity 'u' at an angle 'α' to the horizontal, towards a wall distant 'd' from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is 'e')
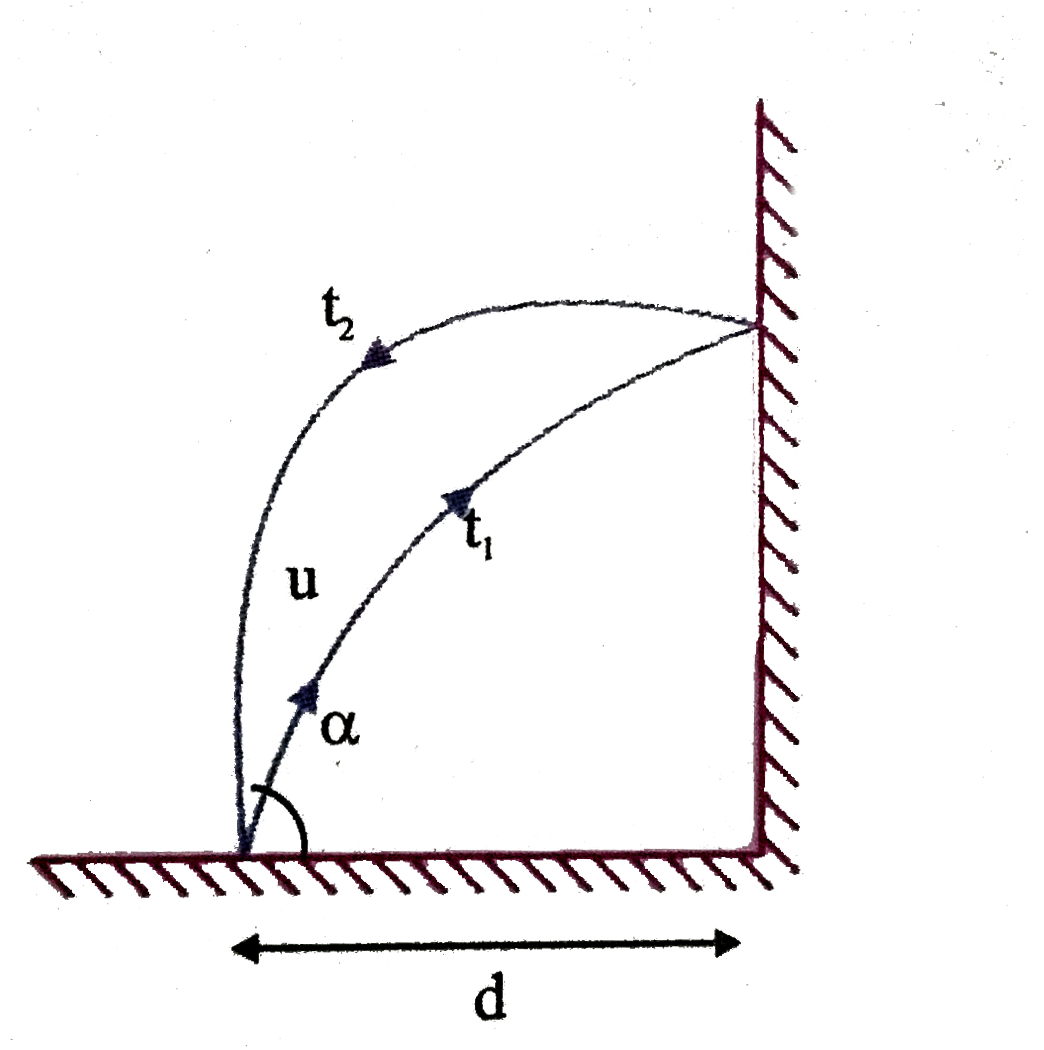
The horizontal distance 'd' from the wall is
View SolutionA ball is dropped on a horizontal surface from height h. If it rebounds upto h2 after first collision then coefficient of restitution between ball and surface is
View Solution
