If →A=2i+3jand→B=2j+3k the component of →B along along →A isSolution in Telugu
6
16
613
6√13
The correct Answer is:D
Step by step video, text & image solution for If vec(A) = 2i + 3j and vec(B) =2 j + 3k the component of vec(B) along along vec(A) is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, POWER & ENERGY BOOK - AAKASH SERIESCHAPTER - WORK, POWER & ENERGY EXERCISE - EXERCISE - II (WORK)
20 Videos
- WORK, POWER & ENERGY BOOK - AAKASH SERIESCHAPTER - WORK, POWER & ENERGY EXERCISE - EXERCISE - II (ENERGY)
33 Videos
- WORK, POWER & ENERGY BOOK - AAKASH SERIESCHAPTER - WORK, POWER & ENERGY EXERCISE - EXERCISE - I
78 Videos
- WORK POWER ENERGYBOOK - AAKASH SERIESCHAPTER - WORK POWER ENERGYEXERCISE - EXERCISE - 3
61 Videos
Similar Questions
The length of a smooth inclined plane of incilination 30∘ is 5 m. The work done is moving a 10kg mass from the bottom of the inclined plane to top is
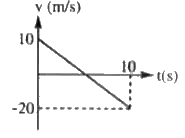
View SolutionVelocity - time graph of a particle moving in a straight line is as shown in figure. Mass of the particle is 2 kg. Work done by all the forces acting on the particle in time interval between t = to t = 10 is
View SolutionIf l1,m1,n1 and l2,m2,n2 are the direction cosines of two vectors and θ is the angle between them, then the value of cos θ is
View SolutionIf →A+→B=→Rand2→A+→B is perpendicular to →B then
View Solutionvec a = i + j + k, vec b = i-j + k, vec c = 2i + 3j-k then (vec aXvec b) Xvec c =
View SolutionWrithe the component of →b along →a.
View SolutionIf vec a=4hat i+6hat j and vec b=3hat j+hat k, then the component of vec a along vec b is
View SolutionGiven →A=3ˆi+2ˆjand→B=ˆi+ˆj. The component of vector →A along vector →B is
View Solution→a=−i+j+2k, →b=2i−j−k and →c=−2i+j+3k ,then the angle between 2→a−→c and →a+→b is
View SolutionWrithe the component of →b along →a.
View Solutionयदि →A=ˆi−2ˆj−3ˆk,→B=2ˆi+ˆj−ˆk,→C=ˆi+3ˆj−2ˆk, तब (→A×→B)×→C=
View SolutionIf vec(A)=2hat(i)+3hat(j) and vec(B)=2hat(j)+3hat(k) the component of vec(B) along bar(A) is
View SolutionThe component of vec(A) along vec(B) is sqrt(3) times that of the component of vec(B) along vec(A) . Then A : B is
View SolutionIf vec(A) = 2i + 3j and vec(B) =2 j + 3k the component of vec(B) along along vec(A) is
View SolutionThe component of →A along →B is √3 times that of the component of →B along →A. Then A: B is
View SolutionThe component of →A along →B is √3 times that of the component of →B along →A. Then A: B is
View Solution
