F=Gm1m2r2 is valid
Between bodies with any shape
Between particles
Between any bodies with uniform density
Between any bodies with same shape
The correct Answer is:A
Similar Questions
∫∞rGm1m2r2dr is equal to
View SolutionAssertion : Mass of the rod AB is m1 and of particle P is m2. Distance between centre of rod and particle is r. Then the gravitational force between the rod and the particle is
F=Gm1m2r2
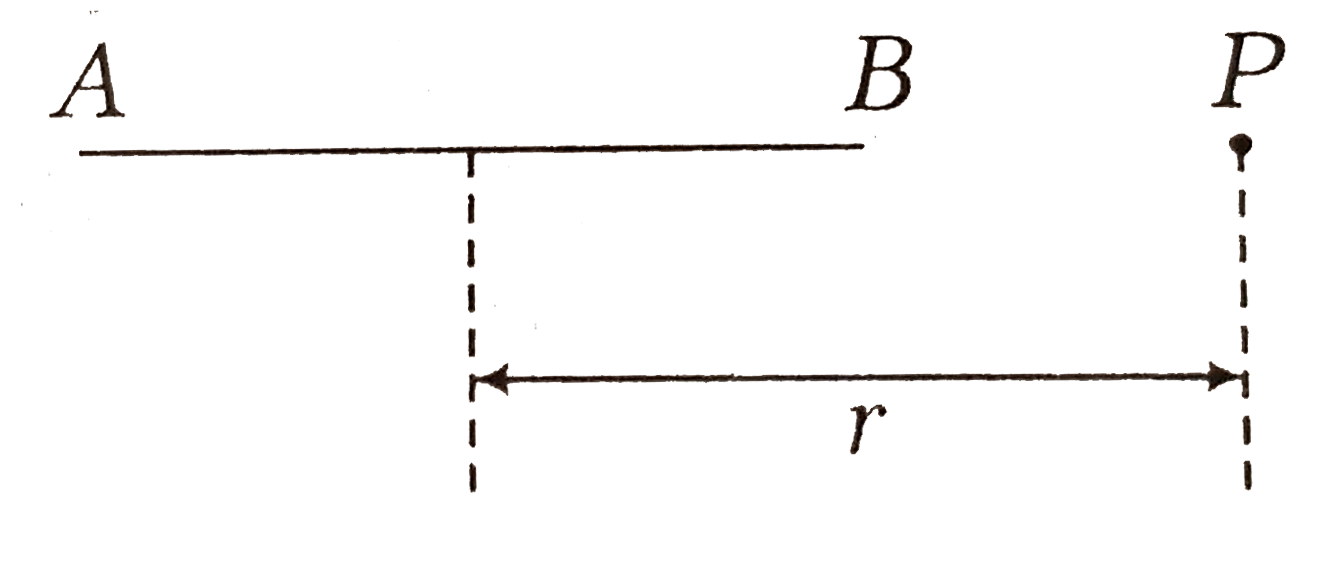
Reason : The relation F=Gm1m2r2 can be applied directly only to find force between two particles.
View Solution
Knowledge Check
f−r2 is valid
Afor convex mirrors but not for concave mirrorsBfor concave mirrors but not for convex mirrorsCfor both convex and concave mirrorsDneither for convex mirrors nor for concave mirrorsWhich one of the following statements is true for the relation F=Gm1m2r2? (All symbols have their usual meanings)
AThe quantity G depends on the local value of g, acceleration due to gravity.BThe quantity G is greatest at the surface of the EarthCThe quantity G is used only when earth is one of the two massesDThe quantity G is a universal constant∫∞rGm1m2r2dr is equal to
AGm1m2rB−Gm1m2r3CGm1m2r3D−Gm1m2r
Find the dimensional formula of the following question :
(a) Surface tension T
(b) Universal constant of gravitation , G
(c ) Impulse ,J
(d) Torque τ
The equation involving these equations are :
T=FilF=Gm1m2r2,J=F×t and τ=F×1
View SolutionFind the dimensional formula of the following question :
(a) Surface tension T
(b) Universal constant of gravitation , G
(c ) Impulse ,J
(d) Torque τ
The equation involving these equations are :
T=FilF=Gm1m2r2,J=F×t and τ=F×1
View SolutionCheck the dimensional consistency of the equation mV2r=Gm1m2r2.
View SolutionGravitational force between two objects with mass m1 and m2 kept r distance apart is given as FG=Gm1m2r2, where G is gravitational constant. Express the relative error in FG.
View SolutionAssertion : Mass of the rod AB is m1 and of particle P is m2. Distance between centre of rod and particle is r. Then the gravitational force between the rod and the particle is
F=Gm1m2r2

Reason : The relation F=Gm1m2r2 can be applied directly only to find force between two particles.
View Solution
