If a planet of radius R and density D is revolving around the sun in a circular orbit of radius r with time period T, then the mass of the sun is

A

$\frac{4 π^{2} r^{3}}{G T}$

B

$\frac{4 π^{2} r^{3}}{G T^{2}}$

C

$\frac{4 π^{2} r}{G T}$

D

$\frac{4 π^{2} r^{3}}{G^{2} T^{2}}$

Text Solution

Verified by Experts

The correct Answer is:B

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Similar Questions

A small planet is revolving around a massive star in a circular orbit of radius R with a period of revolution T. If the gravitational force between the planet and the star were proportional to $R^{- 5 / 2}$ , then T would be proportional to
View Solution
The period of revolution(T) of a planet moving round the sun in a circular orbit depends upon the radius (r) of the orbit, mass (M) of the sun and the gravitation constant (G). Then T is proportioni of $r^{a}$ . The value of a is
View Solution

Knowledge Check

Question 1 - Select One
If a planet of mass $m$ is revolving around the sun in a circular orbit of radius $r$ with time period, $T$ then mass of the sun is
A $4 π^{2} r^{3} / G T$
B $4 π^{2} r^{3} / G T^{2}$
C $4 π^{2} r / G T$
D $4 π^{2} r^{3} / G^{2} T^{2}$
Question 2 - Select One
If a planet revolves around the sun in a circular orbit of radius a with a speed of revolution T, then (K being a positive constant
A $T = K a^{2 / 3}$
B $T = K a^{3 / 2}$
C $T = K a^{2}$
D $T = K a^{3}$
Question 3 - Select One
Many planets are revolving around the fixed sun in circular orbits of different radius $(R)$ and difference time period $(T)$ To estimate the mass of the sun the orbital radius $(R)$ and time period $(T)$ of planets were noted. Then ${log}_{10}$ T v/s ${log}_{10} R$ curve was plotted.
The curve was found to be approximately straight line (as shown in) having y intercept $= 6.0$ (Neglect the gravitational interaction among the planets) [Take $G = \frac{20}{3} \times 10^{- 11}$ in MKS, $π^{2} = 10$ ]

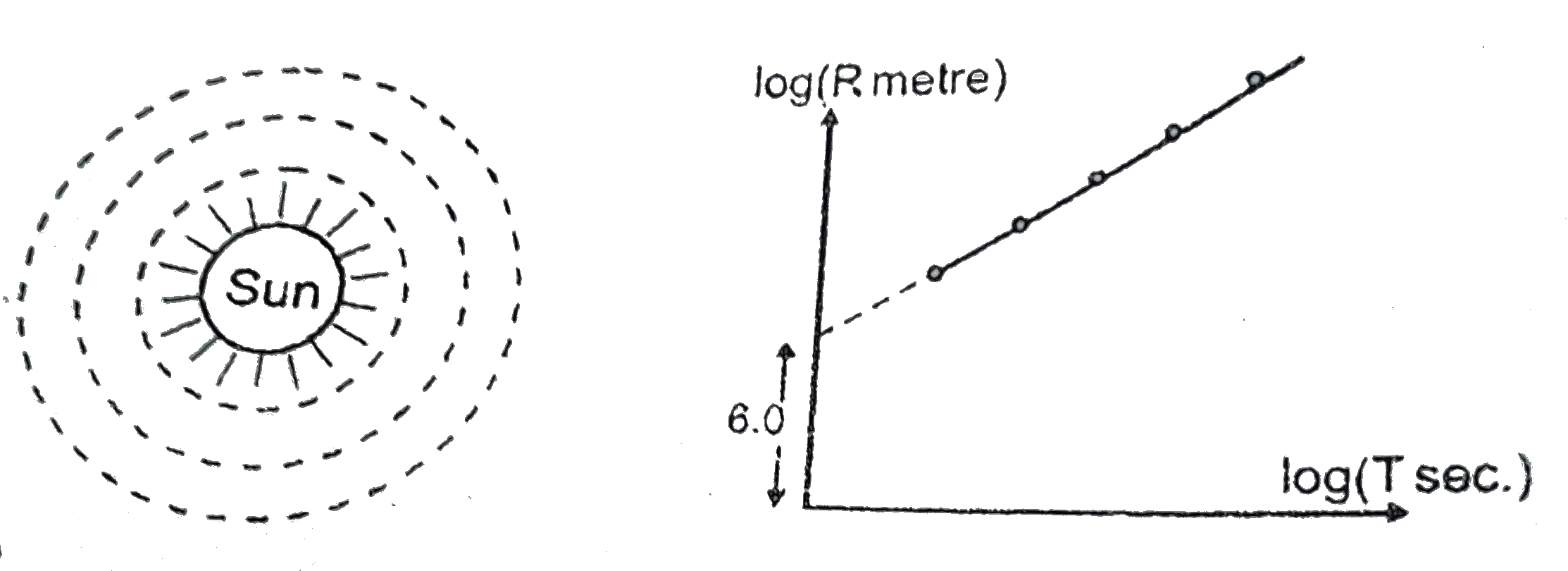
Estimate the mass of the sun .
A $6 \times 10^{29} k g$
B $5 \times 10^{20} k g$
C $8 \times 10^{25} k g$
D $3 \times 10^{35} k g$

Recommended Questions

Home
Ask Doubt
Profile