The area of the region bounded by the curve y=f(x), x-axis, and the lines x=a and x=b where −∞<a<b<−2 is
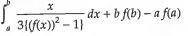
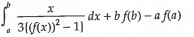
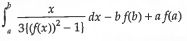
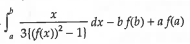
The correct Answer is:A
Step by step video & image solution for The area of the region bounded by the curve y= f( x ), x-axis, and the lines x=a and x=b where -oo lt a lt b lt -2 is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - A DAS GUPTACHAPTER - Some New Pattern ProblemsEXERCISE - Exercise137videos
Some New Pattern Problems
- BOOK - A DAS GUPTACHAPTER - Screening TestsEXERCISE - Exercise38videos
Screening Tests
- BOOK - A DAS GUPTACHAPTER - Total Conditional Probability and Bayes' TheoremEXERCISE - Exercise29videos
Total Conditional Probability and Bayes' Theorem
Similar Questions
Knowledge Check
- Question 1 - Select One
Consider the function defined implicitly by the equation y3−3y+x=0 on various intervals in the real line. If x∈(−∞,−2)∪(2,∞), the equation implicitly defines a unique real-valued defferentiable function y=f(x). If x∈(−2,2), the equation implicitly defines a unique real-valud diferentiable function y−g(x) satisfying g0=0.
The area of the region bounded by the curve y=f(x), the X-axis and the line x=a and x=b, where −∞<a<b<−2 isA∫bax3[{f(x)}2−1]dx+by(b)−af(a)B−∫bax3[{f(x)}2−1]dx−by(b)+af(a)C∫bax3[{f(x)}2−1]dx−by(b)+af(a)D−∫bax3[{f(x)}2−1]dx+by(b)=af(a) - Question 2 - Select One
Consider the function defined implicitly by the equation y3−3y+x=0 on various intervals in the real line. If x∈(−∞,−2)∪(2,∞), the equation implicitly defines a unique real-valued defferentiable function y=f(x). If x∈(−2,2), the equation implicitly defines a unique real-valud diferentiable function y−g(x) satisfying g0=0.
The area of the region bounded by the curve y=f(x), the X-axis and the line x=a and x=b, where −∞<a<b<−2 isA∫bax3[{f(x)}2−1]dx+by(b)−af(a)B−∫bax3[{f(x)}2−1]dx−by(b)+af(a)C∫bax3[{f(x)}2−1]dx−by(b)+af(a)D−∫bax3[{f(x)}2−1]dx+by(b)=af(a) - Question 3 - Select One
Consider the functions defined implicitly by the equation y3−3y+x=0 on various intervals in the real line. If x∈(−∞,−2)∪(2,∞), the equation implicitly defines a unique real-valued differentiable function y=f(x). If x∈(−2,2), the equation implicitly defines a unique real-valued differentiable function y=g(x) satisfying g(0)=0.
The area of the region bounded by the curve y=f(x), the X-axis and the lines x = a and x = b, where −∞<a<b<−2, is :A∫bax3[{f(x)}2−1]dx+bf(b)−af(a)B−∫bax3[{f(x)}2−1]dx+bf(b)−af(a)C∫bax3[{f(x)}2−1]dx−bf(b)+af(a)D−∫bax3[{f(x)}2−1]dx−bf(b)+af(a)
Find the area of the region bounded by the curve y=x2 , the x-axis, and the lines x = 1 and x = 3.
View SolutionFind area of the region bounded by the curve y= −4x, the x-axis and the lines x = −1 and x = -2.
View SolutionConsider the functions defined implicitly by the equationy3–3y+x=0on various intervals in the real line. If x∈(–∞,–2)∪(2,∞), the equation implicitly defines a unique real valued differentiable function y=f(x).Ifx∈(–2,2), the equation implicitly defines a unique real valued differentiable function y = g(x) satisfying g(0) = 0
The area of the region bounded by the curve y = f(x), the x-axis and the lines x = a and x = b, where –∞<a<b<–2, isView SolutionThe area of the region bounded by the curve y=cosx, X-axis and the lines x=0, x=2π is
View SolutionThe area of the region bounded by the curve y=x2 and the line y=16 is :
View Solution

