Let s be the sum of all distinct real roots of f(x) and let t=mod(s)The area bounded by the curve y=f(x) and the lines x=0,y=0 and x=t, lies in the interval
(34,3)
(2164,11,16)
(9,10)
(0,2164)
The correct Answer is:A
Step by step video & image solution for Let s be the sum of all distinct real roots of f(x) and let t=mod(s)The area bounded by the curve y= f(x) and the lines x=0, y=0 and x=t, lies in the interval by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - A DAS GUPTACHAPTER - Some New Pattern ProblemsEXERCISE - Exercise137videos
Some New Pattern Problems
- BOOK - A DAS GUPTACHAPTER - Screening TestsEXERCISE - Exercise38videos
Screening Tests
- BOOK - A DAS GUPTACHAPTER - Total Conditional Probability and Bayes' TheoremEXERCISE - Exercise29videos
Total Conditional Probability and Bayes' Theorem
Similar Questions
Knowledge Check
- Question 1 - Select One
Let f(x) be a continuous function such that the area bounded by the curve y=f(x), the x-axis, and the lines x=0 and x=ais1+a22sin a. Then,
A(π2)=1+π28Bf(a)=1+a22sinaCf(a)=asina+12cosaDnone of these - Question 2 - Select One
Let f(x)=x2/3,x≥0. Then the area of the region enclosed by the curve y=f(x) and the three lines y=x,x=1andx=8 is
A632B935C1057D12910 - Question 3 - Select One
Let g(x)=cosx2,f(x)=√x, and α,β(α<β) be the roots of the quadratic equation 18x2−9πx+π2=0. Then the area (in sq. units) bounded by the curve y=(gof)(x) and the lines x=α,x=β and y=0 is
A12(√3−√2)B12(√3−1)C12(√3−1)D12(√3+1)
Let
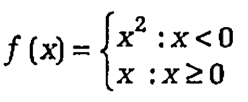 .Area bounded by the curve y=f(x),y=0andx2=9a2is9a2 Then a= …..............View Solution
.Area bounded by the curve y=f(x),y=0andx2=9a2is9a2 Then a= …..............View SolutionIf the area bounded by y=f(x), the x-axis, the y-axis and x=t(t>0) is t2, then find f(x).
View SolutionLet f (x) be a continous function such that the area bounded by the curve y=f(x) x-axis and the lines x=0 and x=aisa22+a2sina+π2cosa, then f(π2) is
View SolutionConsider the polynomial f(x)=1+2x+3x2+4x3. Let s be the sum of all distinct real roots of f(x)and let t=|s|.
View SolutionConsider the polynomial f(x)=1+2x+3x2+4x3. Let s be the sum of all distinct real roots of f(x) and let t=|s|.
View Solution

